机器学习之机器学习概述

机器学习基本分类，学习方法三要素

机器学习概述

• 机器学习（machine learning）是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科。
• 研究对象：数据（data） -数字、文字、图像、视频、音频以及他们的组合
• 基本假设：同类数据具有一定的统计规律性。
• 机器学习的应用：计算机视觉、自然语言处理、语音工程、规划决策、数据挖掘

机器学习分类

基本分类：

• 监督学习（supervised learning）
• 无监督学习（unsupervised learning）
• 强化学习（reinforcement learning）
• 半监督学习（semi-supervised learning）
• 主动学习（active learning）

模型分类：

• 概论模型 vs 非概率模型
• 线性模型 vs 非线性模型
• 参数化模型 vs 非参数化模型

监督学习

监督学习（supervised learning）是指从标注数据中学习预测模型的机器学习问题。

标注数据-==表示输入输出的对应关系==；

• 数据集（data）：所有记录的集合。
• 样本（sample）： 每一条记录
• 特征（feature）/属性（attribute）：反映事件或对象在某方面的表现或者性质的事项。 例如：色泽、敲声
• 样本空间：由属性张成的空间
• 属性值：属性上的取值

预测模型-==对给定的输入产生相应输出==；

• 训练集（training set）：所有训练样本的集合
• 测试集（test set）：所有测试样本的集合
• 泛化能力（generalization）: 机器学习出来的模型适用于新样本的能力， 即从特殊到一般。

标注数据-表示输入输出的对应关系；

预测模型-对给定的输入产生相应输出；

监督学习的本质-==学习输入到输出映射的统计规律==。

无监督学习

无监督学习（unsupervised learning）是指从无标注数据中学习预测模型的机器学习问题。

无监督学习的本质-==学习数据中的统计规律或潜在结构==。

机器学习三要素

方法 = 模型 + 策略 + 算法

• 模型： 输入和输出之间的“映射”关系
• 策略： 按照什么样的准则学习或选择最优的模型
• 算法： 具体的计算方法求解最优模型/模型参数估计方法(基本下降算法：最速下降法、牛顿法)

模型的选择与评估

训练误差和测试误差

机器学习模型的输出结果与其对应的真实值之间往往会存在一定的差异，这种差异被称为模型的输出误差，简称为误差。

• 训练样本：用于构造模型的样本
• 训练误差(经验风险,training error)：指模型在训练样本集上的整体误差
• 测试样本：用于测试模型效果的样本
• 测试误差(test error)：模型在测试样本集上的整体误差
• 泛化能力(generalization ability)：将学习方法对于未知数据的预测能力
• 泛化误差：对于某个给定的机器学习任务，假设与该任务相关的所有样本构成的样本集合为$𝐷$，则机器学习模型在样本集合$𝐷$上的整体误差。

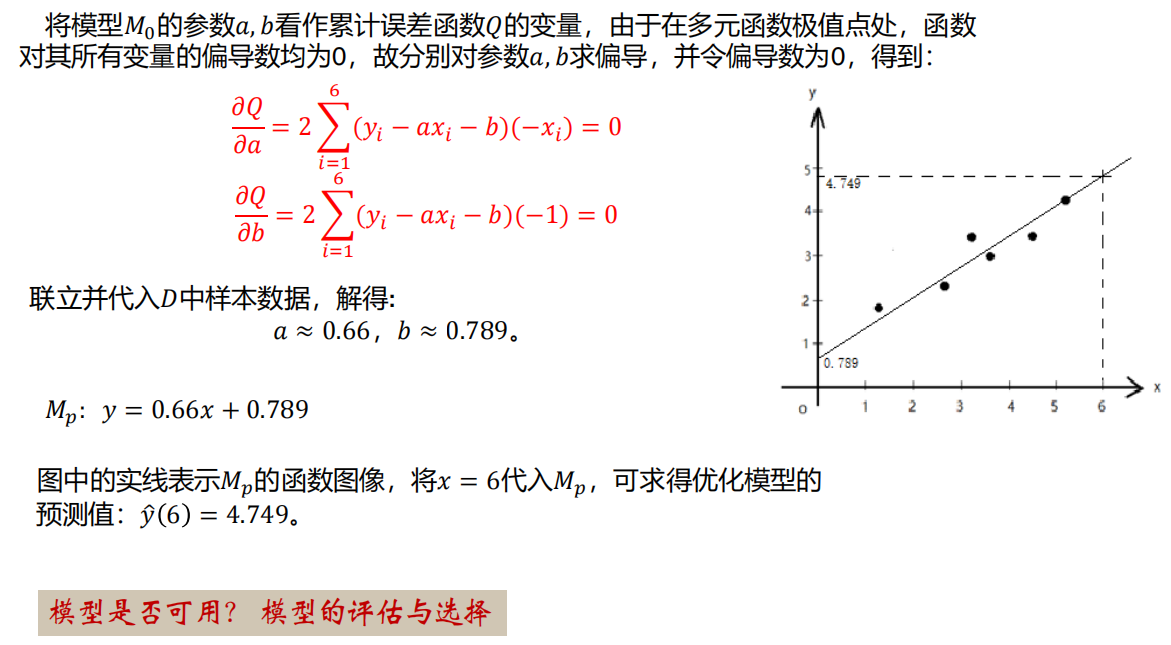
• 满足条件的模型通常不止一个，此时需要对多个满足条件的映射做出选择。
• 选择的主观倾向性称为机器学习算法的模型偏好。
• 奥卡姆剃刀原则：在同等条件下选择简单事物的倾向性原则。

泛化误差VS测试误差

在学习方法实现过程中，可采用测试误差近似泛化误差

泛化误差越小越好！训练误差过小可能会导致过拟合

训练集和测试集的划分

测试集(test set)应该与训练集(training set)“互斥” , 即测试样本尽量不在训练集中出现、未在训练过程中使用过。

常见方法：

• 留出法(hold-out)
• 交叉验证(cross validation)
• 自助法(bootstrap)

留出法

• 保持训练集和测试集数据分布一致性； 例：60% 好瓜，40%不好
• 多次重复划分 (例如: 100次随机划分)
• 测试集不能太大、不能太小 (例如：1/5-1/3)

优点：简单；缺点：训练集和测试集的比例不好划分

交叉验证法

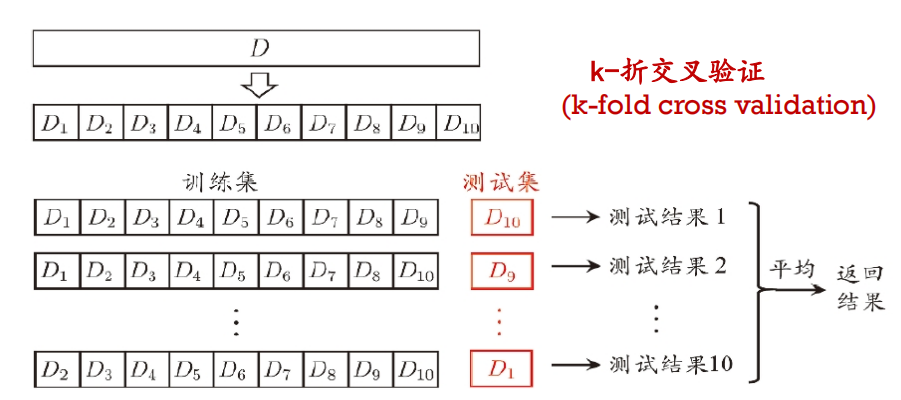
优点：评估结果相对精确；缺点：数据集大时，计算成本高

自助法

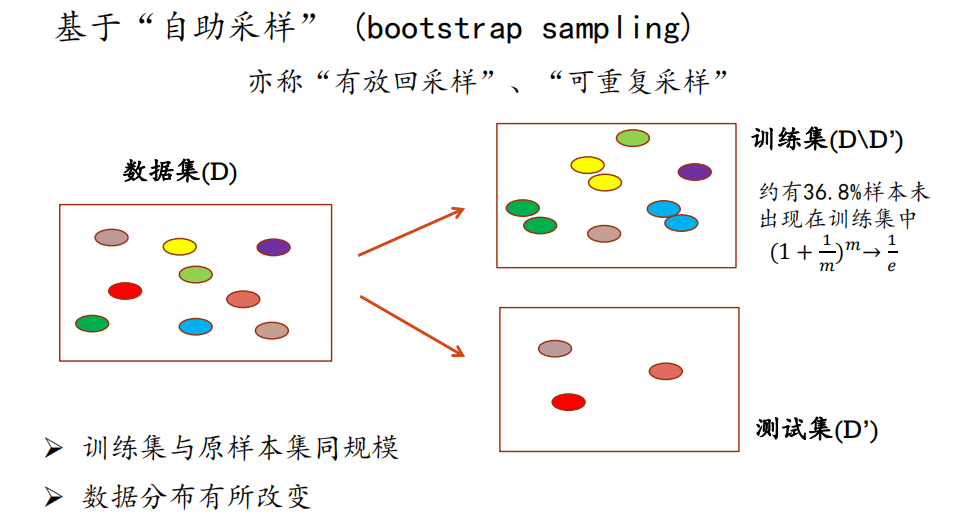
优点：不改变数据集规模，适用于小样本问题；缺点：改变了数据集分布，引入估计偏差

数据集划分小结：

• 改变数据集的规模：留出法、交叉验证法
• 改变数据集的分布：自助法

监督学习概论

损失函数和风险函数（假设：空间中选取模型$𝑓$ 做为决策函数）

损失函数/代价函数（loss function）：度量预测错误的程度 $𝐿(𝑦_𝑖, 𝑓(𝑥_𝑖))$

常见的损失函数：

风险函数

策略：最小化经验/结构经验

正则化（regularization）：是结构化风险最小化策略的实现

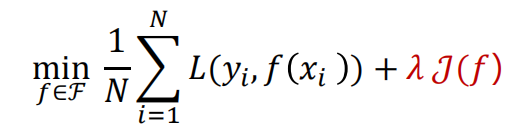
模型的选择和评估：训练误差与测试误差

模型参数估计方法

基本下降算法：最速下降法、牛顿法

最速下降法

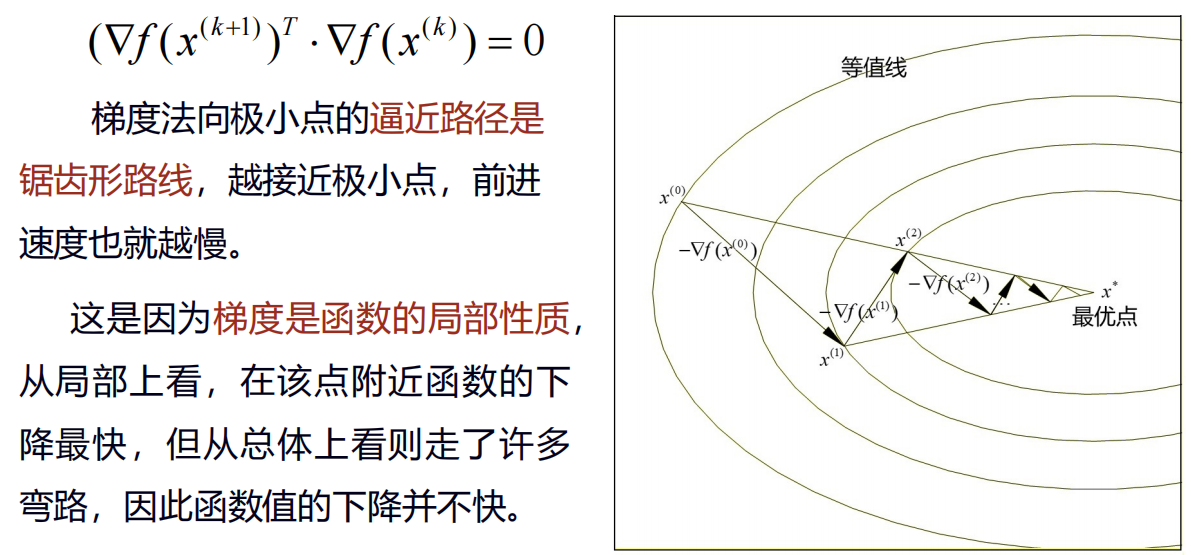
梯度方向与函数 $f$ 的等值线的一个法线方向相同，就是函数 $f$ 的值增加最快的方向，梯度反方向就是函数值降低最快的方向，采用负梯度矢量作为一维搜索的方向，因而又称作最速下降法。

最速下降法又称为梯度法，由Cauchy于1847年给出。最速下降法解决的是具有连续可微的目标函数的无约束极值问题迭代过程简单，使用方便。

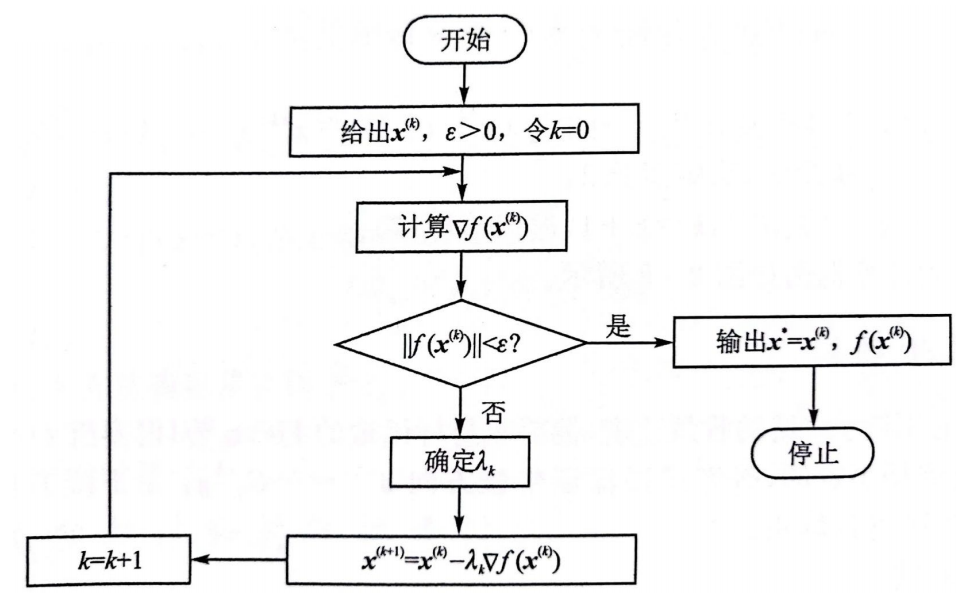
特点

• 优点：程序结构简单，每次迭代所需的计算量及存储量也小，而且当迭代点离最优点较远时函数值下降速度很快。
• 缺点：在迭代点到达最优点附近时，进展十分缓慢，而且常常由于一维搜索的步长误差而产生的挠动不可能取得较高的收敛精度。

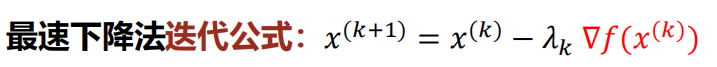
牛顿法

阻尼牛顿法（重点）

算法步骤：

例题