强化学习之算法【补充】

发表于 更新于 分类于 阅读次数： Valine： 本文字数： 6.8k 阅读时长 ≈ 6 分钟
PER DQN、Dueling DQN、Policy Gradients、Reinforce、Actor Critic、DDPG、A3C（不适合入门，因为这属于我入门后期的总结）。跟随莫烦python的视频和代码，并将其改成Pytorch版本。

Prioritized Experience Replay（DQN）

在原始的DQN算法中，改进提取记忆库的代码，将原本batch的随机抽样，改成按照 Memory 中的样本优先级来抽，所以这能更有效地找到我们需要学习的样本

伪代码

PER DQN伪代码

优先级确认方式：

优先级确认方式

用到 TD-error, 也就是 Q现实 - Q估计 来规定优先学习的程度。如果 TD-error 越大, 就代表我们的预测精度还有很多上升空间, 那么这个样本就越需要被学习, 也就是优先级 p 越高。当最开始并不知道TD-error时，默认为最大，可保证所有经验最少能回放一次。

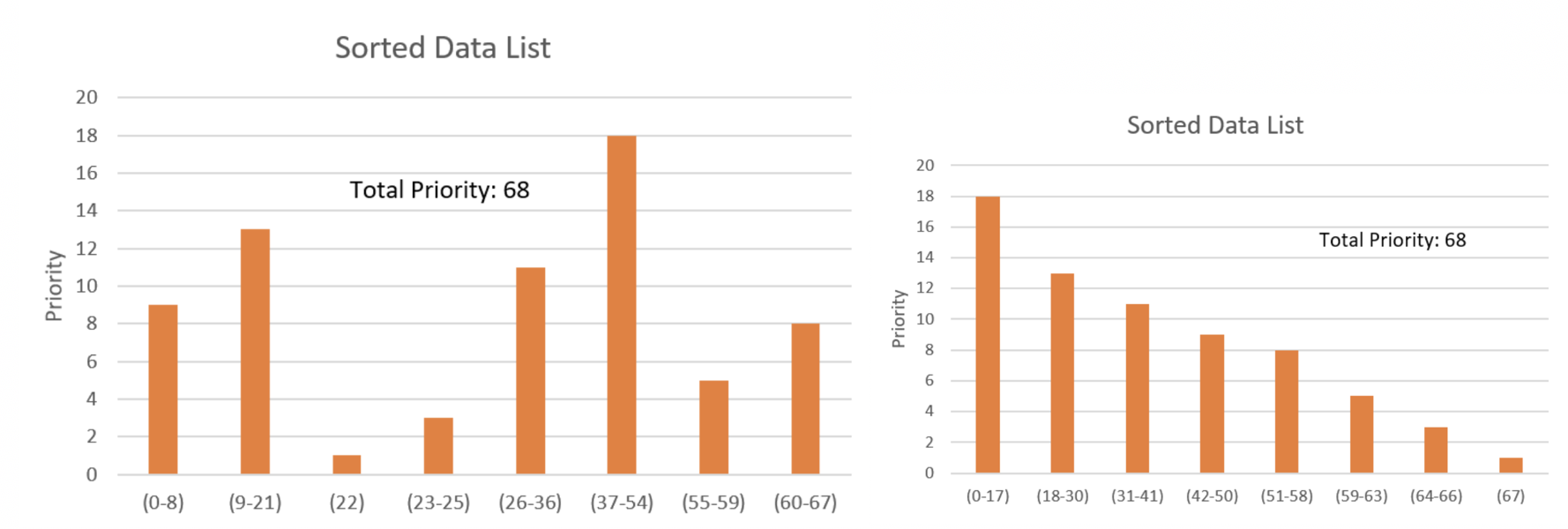
根据 p的抽样方式：SumTree

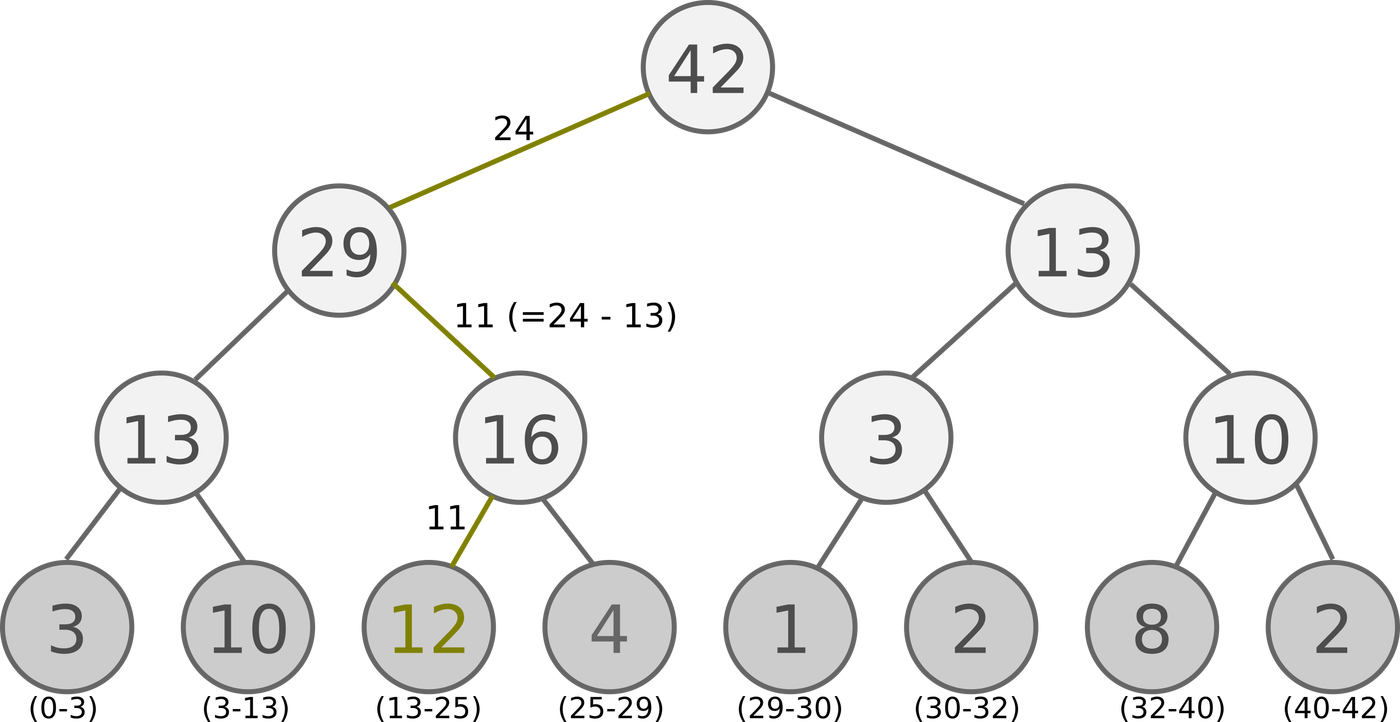
PER sumTree

对上图的理解，叶子结点中的数字代表的是一个范围（上图最底下），范围越大，抽中的概率也就越大，也就达到了按照重要程度来抽样的目的

代码：

self.abs_errors = torch.sum(torch.abs(q_target - q_eval)：计算优先级，优先级实际上为loss的绝对值

tree_idx, batch_memory, ISWeights = self.memory.sample(self.batch_size)：从memory类中的samples方法中获取，因为事先有tree_id，因此不存在重复抽样的问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def learn(self):
    ...

    if self.prioritized:
        tree_idx, batch_memory, ISWeights = self.memory.sample(self.batch_size)
    else:
        sample_index = np.random.choice(self.memory_size, size=self.batch_size)
        batch_memory = self.memory[sample_index, :]

    ...    
    if self.prioritized:
        self.abs_errors = torch.sum(torch.abs(q_target - q_eval), dim=1)
        # print("ISWeights shape: ", ISWeights.shape, 'q shape: ', ((q_target-q_eval)**2), 'q: ', (q_target-q_eval))
        loss = torch.mean(torch.mean(torch.Tensor(ISWeights) * (q_target - q_eval) ** 2, dim=1))
        self.memory.batch_update(tree_idx, self.abs_errors)
    else:
        self.loss_func = nn.MSELoss()
        loss = self.loss_func(q_eval, q_target)

    # print("loss: ", loss, self.prioritized)
    ...

在Memory类中，包含两个主要的函数：store和sample。其中store用于将每次的状态转移存储到内存中，sample则用于从内存中取出一定数量的状态转移（通常称为batch）以供训练使用。

1
2
3
4
5
6
7
8
9
class Memory(object):  # stored as (s, a, r, s_) in SumTree
    # 建立 SumTree 和各种参数
    def __init__(self, capacity):
    # 存储数据, 更新 SumTree
    def store(self, transition):
    # 抽取 sample
    def sample(self, n):
    # train 完被抽取的 samples 后更新在 tree 中的 sample 的 priority
    def batch_update(self, tree_idx, abs_errors):

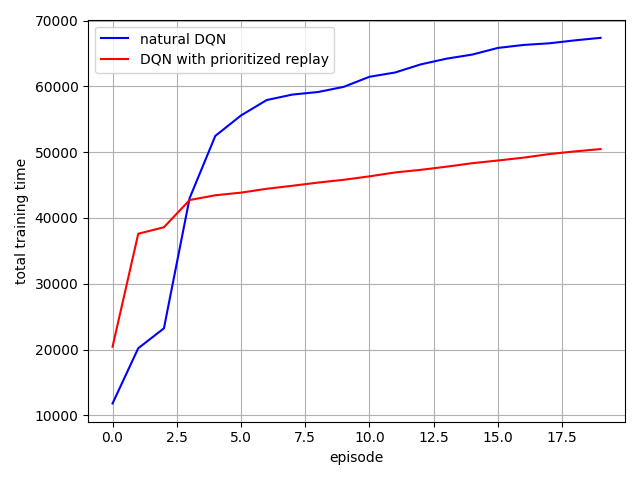
PER DQN实验结果

**总结：**在抽取经验池中过往经验样本时，采取按优先级（TD-error）抽取的方法，引入sum-tree（范围制随机抽样，优先级越高越有可能被抽中）。使得算法更快收敛，效果更好。

疑问：

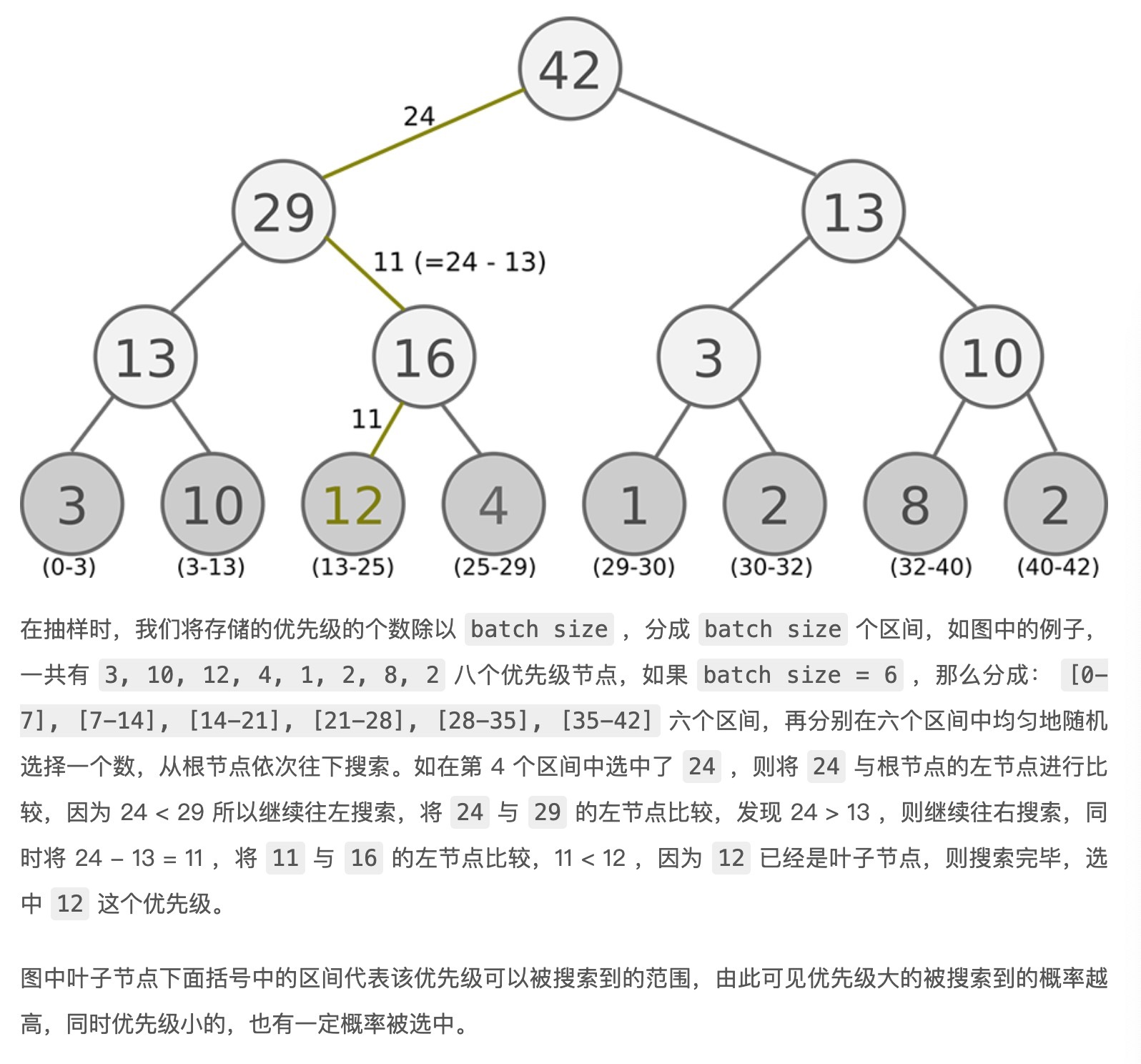
如果说在第4区间选中了24，最终抽样会得到12，那如果在第三区间选中了20，那最终抽样也是12呀，这样不会导致memory重复吗？如果是会覆盖的话，那是不是会一直找，直到达到batch_size？

Dueling DQN

将每个动作的 Q 拆分成了 state 的 Value 加上 每个动作的 Advantage

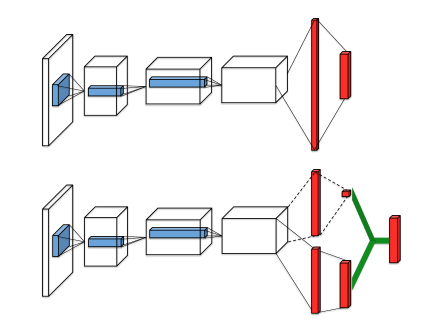
Dueling DQN网络结构

在DQN算法的网络结构中，输入为一张或多张照片，利用卷积网络提取图像特征，之后经过全连接层输出每个动作的动作价值；

在Dueling DQN算法的网络结构中，输入同样为一张或多张照片，然后利用卷积网络提取图像特征获取特征向量，输出时会经过两个全连接层分支，分别对应状态价值和优势值，最后将状态价值和优势值相加即可得到每个动作的动作价值(即绿色连线操作)。

原来 的DQN 神经网络直接输出的是每种动作的 Q值, 而 Dueling DQN 每个动作的 Q值 是由下面的公式确定的：分别是该状态的状态价值V(标量)和每个动作的优势值A(与动作空间同维度的向量)

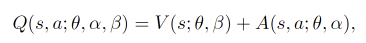
提出原因来自一个赛车游戏例子：当前方没有车辆时，智能体左右移动并没有影响，说明动作对Q值没有影响，但是状态对Q值很有影响。当前方存在车辆阻挡时，智能体的动作选择至关重要，说明动作对Q值存在影响，同样状态对Q值也会存在影响。

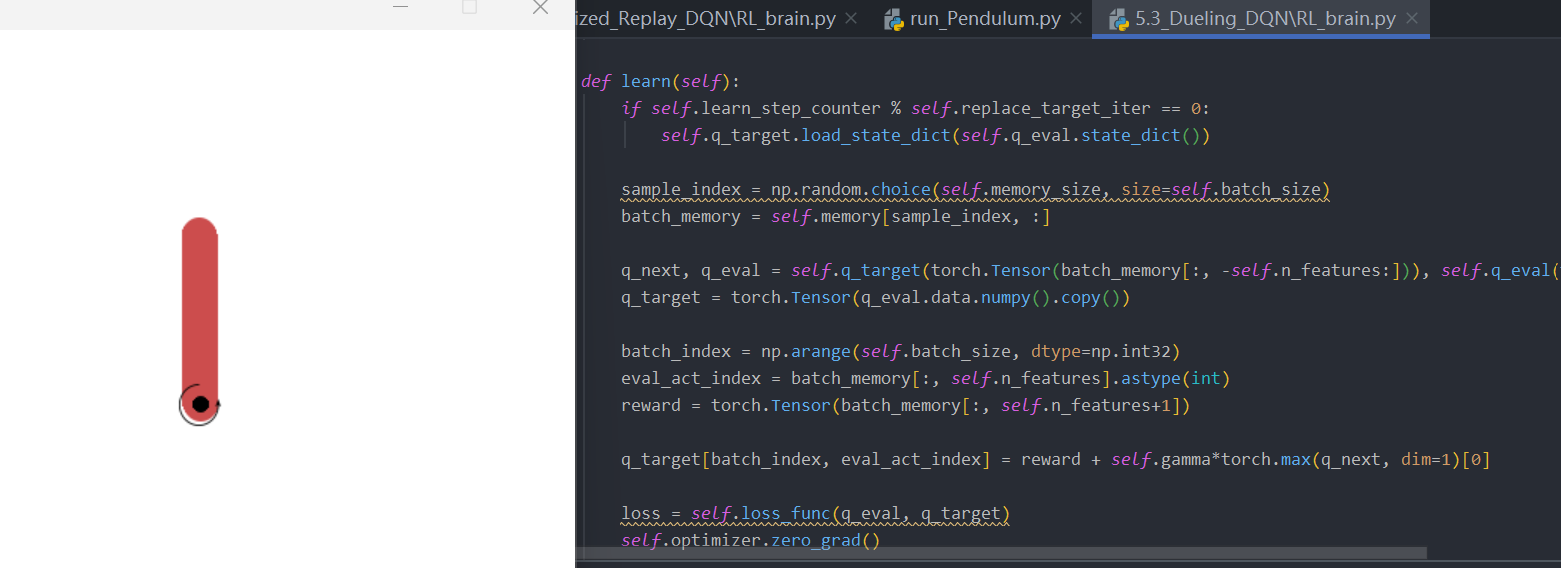
代码：

在神经网络代码中，明确写出有两个全连接层：self.values、self.advantages

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Net(nn.Module):
	def __init__(self, n_feature, n_hidden, n_output, dueling=False):
		super(Net, self).__init__()
		self.dueling = dueling
		self.l1 = nn.Linear(n_feature, n_hidden)
		if self.dueling:
			self.values = nn.Linear(n_hidden, 1)
			self.advantages = nn.Linear(n_hidden, n_output)
		else:
			self.q = nn.Linear(n_hidden, n_output)

	def forward(self, x):
		x = self.l1(x)
		x = F.relu(x)
		if self.dueling:
			value = self.values(x)
			advantages = self.advantages(x)
			out = value + (advantages-torch.mean(advantages, dim=1, keepdim=True))
		else:
			out = self.q(x)
		return out

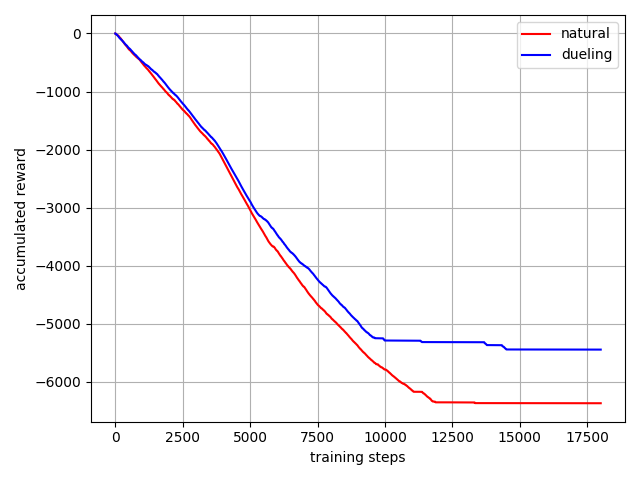
**总结：**通过改进神经网络最终的全连接输出，从一个输出Q值改进为输出状态V值和动作A值，加强算法收敛能力。

Policy Gradients——策略

对比以值为基础的方法, Policy Gradients 直接输出动作的最大好处就是, 它能在一个连续区间内挑选动作（根据所学习到的动作分布随机进行筛选）, 而基于值的, 比如 Q-learning, 它如果在无穷多的动作中计算价值, 从而选择行为, 这, 它可吃不消。

Policy Gradients 没有误差概念，其反向传递的目的是让这次被选中的行为更有可能在下次发生。

核心思想：

观测的信息通过神经网络分析, 选出了左边的行为, 我们直接进行反向传递, 使之下次被选的可能性增加, **但是奖惩信息却告诉我们, 这次的行为是不好的, 那我们的动作可能性增加的幅度随之被减低。即，**靠奖励来左右我们的神经网络反向传递

Reinforce方法（基于整条回合数据的更新）

policy gradient 的最基本方法

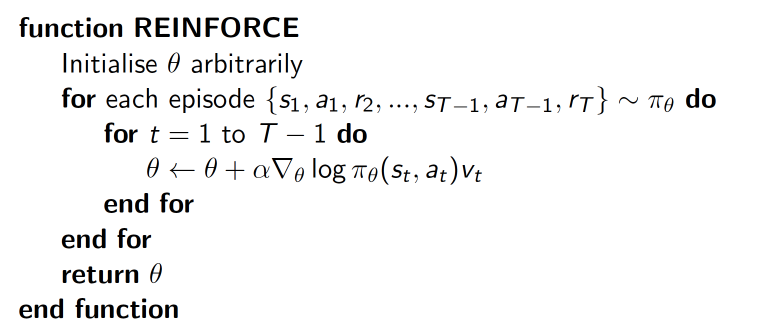
Reinforce伪代码

delta(log(Policy(s,a))*V) ：表示在 状态 s 对所选动作 a 的吃惊度。

如果 Policy(s,a) 概率越小，反向的 log(Policy(s,a)) (即 -log(P)) 反而越大。如果在 Policy(s,a) 很小的情况下，拿到了一个 大的 R, 也就是 大的 V, 那-delta(log(Policy(s, a))*V) 就更大, 表示更吃惊， (我选了一个不常选的动作, 却发现原来它能得到了一个好的 reward, 那我就得对我这次的参数进行一个大幅修改）

tip：选log的原因是因为在值很小的时候梯度很大，便于学习。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class PolicyGradient:
    # 初始化 (有改变)
    def __init__(self, n_actions, n_features, learning_rate=0.01, reward_decay=0.95, output_graph=False):

    # 建立 policy gradient 神经网络 (有改变)
    def _build_net(self):

    # 选行为 (有改变)
    def choose_action(self, observation):

    # 存储回合 transition (有改变)——回合的记忆，不是记忆库
    def store_transition(self, s, a, r):

    # 学习更新参数 (有改变)
    def learn(self, s, a, r, s_):

    # 衰减回合的 reward (新内容)
    def _discount_and_norm_rewards(self):

**总结：**是为了解决无穷动作的情况而提出的，更适合连续的空间（缺点：因PG是每回合更新，以值为基础的算法能进行单步更新，因此学习效率降低）

Actor Critic

结合以值为基础（如Q-Learning）和以动作概率为基础（如Policy Gradients）两类算法。Actor 基于概率选行为，Critic 基于 Actor 的行为评判行为的得分，Actor 根据 Critic 的评分修改选行为的概率

  • Actor——Policy Gradients；
  • Critic——Q-Learning

因为PG算法的回合更新问题，提出改进算法AC：可以进行单步更新, 比传统的 Policy Gradient 要快；但是取决于 Critic 的价值判断, 但是 Critic 难收敛, 再加上 Actor 的更新, 就更难收敛。

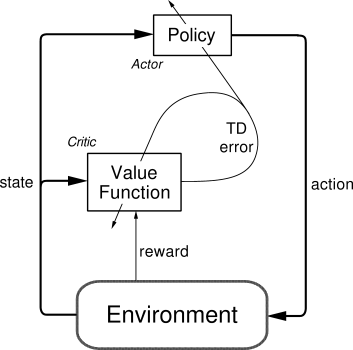
Actor 修改行为时就像蒙着眼睛一直向前开车, Critic 就是那个扶方向盘改变 Actor 开车方向的。

也就是说， Actor 在运用 Policy Gradient 的方法进行 Gradient ascent 的时候, 由 Critic 来告诉他, 这次的 Gradient ascent 是不是一次正确的 ascent, 如果这次的得分不好, 那么就不要 ascent 那么多（就是套娃）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Actor(object):
    def __init__(self, sess, n_features, n_actions, lr=0.001):
        # 用 tensorflow 建立 Actor 神经网络,
        # 搭建好训练的 Graph.

    def learn(self, s, a, td):
        # s, a 用于产生 Gradient ascent 的方向,
        # td 来自 Critic, 用于告诉 Actor 这方向对不对.

    def choose_action(self, s):
        # 根据 s 选 行为 a
...
class Critic(object):
    def __init__(self, sess, n_features, lr=0.01):
        # 用 tensorflow 建立 Critic 神经网络,
        # 搭建好训练的 Graph.

    def learn(self, s, r, s_):
        # 学习 状态的价值 (state value), 不是行为的价值 (action value),
        # 计算 TD_error = (r + v_) - v,
        # 用 TD_error 评判这一步的行为有没有带来比平时更好的结果,
        # 可以把它看做 Advantage
        return # 学习时产生的 TD_error

Actor 想要最大化期望的 reward，在 Actor Critic 算法中，用“比平时好多少” (TD error) 来当做 reward；

Critic 的更新很简单，就是像 Q learning 那样更新现实和估计的误差 (TD error) 就好了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Actor	
def learn(self, s, a, td):
	s = torch.Tensor(s[np.newaxis, :])
	acts_prob = self.actor_net(s)
	log_prob = torch.log(acts_prob[0, a])
	exp_v = torch.mean(log_prob * td)

	loss = -exp_v
	self.optimizer.zero_grad()
	loss.backward(retain_graph=True)
	self.optimizer.step()

	return exp_v
# Critic
def learn(self, s, r, s_):
	s, s_ = torch.Tensor(s[np.newaxis, :]), torch.Tensor(s_[np.newaxis, :])
	v, v_ = self.critic_net(s), self.critic_net(s_)
	td_error = r + GAMMA * v_ - v
	loss = td_error ** 2

	self.optimizer.zero_grad()
	loss.backward(retain_graph=True)
	self.optimizer.step()

	return td_error

**总结：**类似套娃，先用actor网络去求出当前状态下每个动作的概率，再引进critic网络来对actor网络做参数调整的约束。但是取决于 Critic 的价值判断, 但是 Critic 难收敛, 再加上 Actor 的更新, 就更难收敛。

DDPG

DDPG = Actor Critic + DQN

在AC算法上的改进算法，解决难收敛的问题（在连续空间上更新，相关性较大），提出DDPG算法（Deep Deterministic Policy Gradient）

概念上理解可以分为下图：

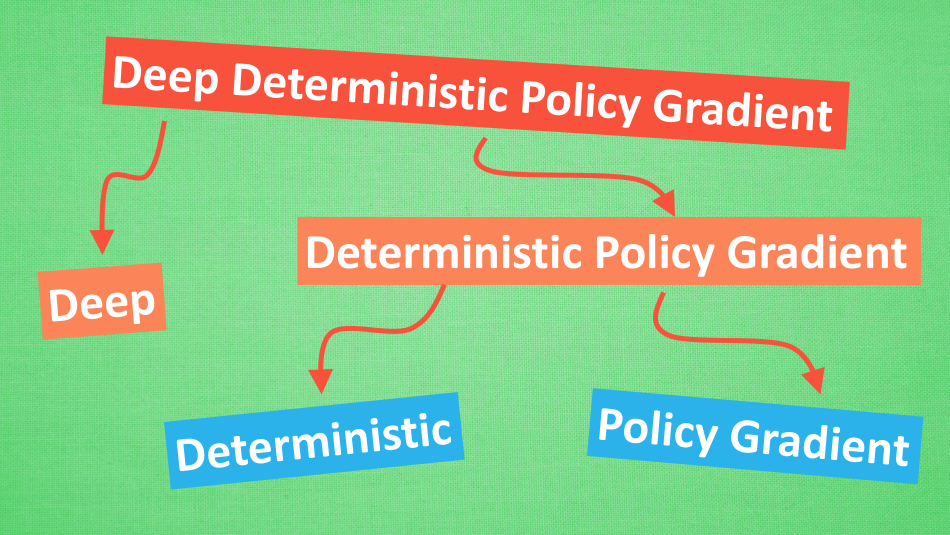
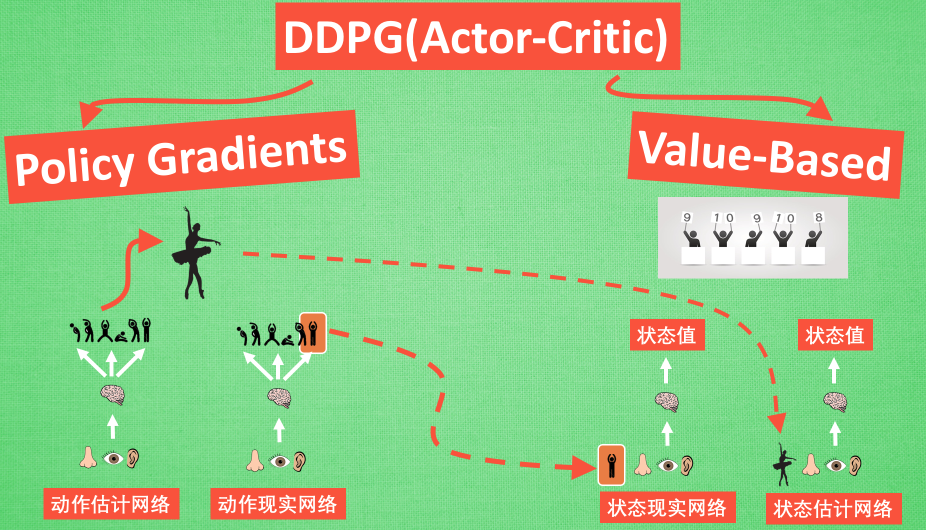
神经网络理解上可以分为下图：

  1. 和Actor-Critic 形式差不多, 也需要有基于策略 Policy 的神经网络和基于价值 Value 的神经网络。

  2. 但是为了体现 DQN 的思想, 每种神经网络都需要再细分为两个：

    • Policy Gradient 这边, 有估计网络和现实网络, 估计网络用来输出实时的动作, 供 actor 在现实中实行. 而现实网络则是用来更新价值网络系统的.

    • 价值系统这边, 也有现实网络和估计网络, 他们都在输出这个状态的价值, 而输入端却有不同, 状态现实网络这边会拿着从动作现实网络来的动作加上状态的观测值加以分析, 而状态估计网络则是拿着当时 Actor 施加的动作当做输入.

在实际运用中, DDPG 的这种做法的确带来了更有效的学习过程.

Actor参数更新：

前半部分 grad[Q] 是从 Critic 来的, 这是在说: 这次 Actor 的动作要怎么移动, 才能获得更大的 Q, 而后半部分 grad[u] 是从 Actor 来的, 这是在说: Actor 要怎么样修改自身参数, 使得 Actor 更有可能做这个动作. 所以两者合起来就是在说: Actor 要朝着更有可能获取大 Q 的方向修改动作参数了

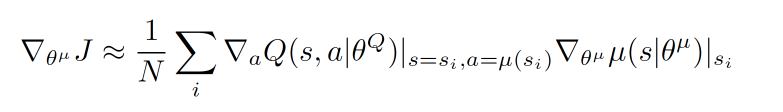
Actor参数更新公式

Critic参数更新

借鉴 DQN 和 Double Q learning 的方式, 有两个计算 Q 的神经网络, Q_target 中依据下一状态, 用 Actor 来选择动作, 而这时的 Actor 也是一个 Actor_target (有着 Actor 很久之前的参数). 使用这种方法获得的 Q_target 能像 DQN 那样切断相关性, 提高收敛性

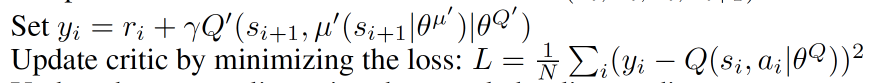
Critic参数更新公式

总结：一种使用 Actor Critic的结构, 但是输出的不是行为的概率, 而是具体的行为, 用于连续动作 (continuous action) 的预测. DDPG 结合了之前获得成功的 DQN 结构, 提高了 Actor Critic 的稳定性和收敛性。

A3C

依旧是为解决AC算法不收敛的问题，提出A3C算法（Asynchronous Advantage Actor-Critic）。

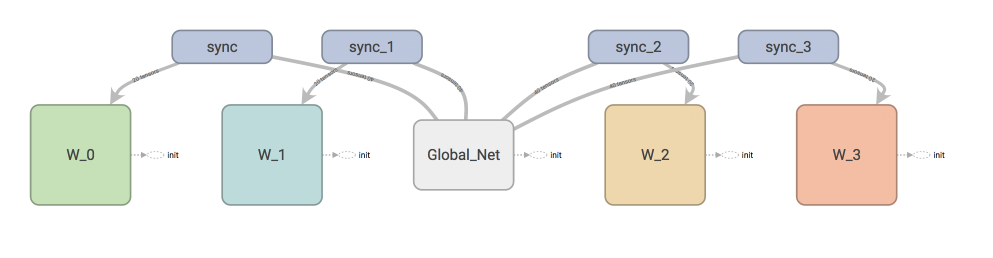
会创建多个并行的环境, 让多个拥有副结构的 agent 同时在这些并行环境上更新主结构中的参数. 并行中的 agent 们互不干扰, 而主结构的参数更新受到副结构提交更新的不连续性干扰, 所以更新的相关性被降低, 收敛性提高

伪代码：

有两套体系, 可以看作中央大脑拥有 global net 和他的参数, 每位玩家有一个 global net 的副本 local net, 可以定时向 global net 推送更新, 然后定时从 global net 那获取综合版的更新。

A3C网络结构