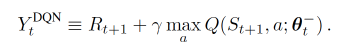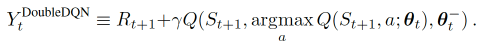强化学习之算法

发表于 更新于 分类于 阅读次数： Valine： 本文字数： 7.8k 阅读时长 ≈ 7 分钟
Q-Learning、Sarsa、Sarsa（Lambda）、DQN、Double DQN（不适合入门，因为这属于我入门后期的总结）。跟随莫烦python的视频和代码，并将其改成Pytorch版本。

Q-Learning和Sarsa的区别

Q-Learning会在做动作前先观望（更新Q表的Q值），例如在s1状态时就已经估算了在s2选择动作的Q值，但实际上到了s2时因为在s1时更新了Q表，所以并不一定会选择之前计算出的最大Q值；

Sarsa会在计算出Q值之后直接选择动作

伪代码

代码

其中对应上图中橙色区域为（a_为在前一个状态得到的当前最大Q值动作）

​ -Q-Learning：q_target = r + self.gamma * self.q_table.loc[s_, :].max()

​ -Saras：q_target = r + self.gamma * self.q_table.loc[s_, a_]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# off-policy
class QLearningTable(RL):
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        super(QLearningTable, self).__init__(actions, learning_rate, reward_decay, e_greedy)

    def learn(self, s, a, r, s_):
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, :].max()  # next state is not terminal
        else:
            q_target = r  # next state is terminal
        self.q_table.loc[s, a] += self.lr * (q_target - q_predict)  # update


# on-policy
class SarsaTable(RL):

    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        super(SarsaTable, self).__init__(actions, learning_rate, reward_decay, e_greedy)

    def learn(self, s, a, r, s_, a_):
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, a_]  # next state is not terminal
        else:
            q_target = r  # next state is terminal
        self.q_table.loc[s, a] += self.lr * (q_target - q_predict)  # update

总结：

  1. Q-learning 在learn的时候，用的是Max的方法，所以学的一定是最大的。但是在choose 的时候因为epsilon而存在随机性，下一个更新的不一定是最大回报对应的action。但每次更新的回报一定是max的。
  2. Sarsa 在learn之前用epsilon choose了action，并且确定用这个action进行learn。所以learn的不一定是最大回报的。但step的action和learn的一定是同一个。
  3. 所以说Q-learning一定学max，更激进。

  • Q-Learning像是一个勇士，永远朝效果最好的方向走去，不用担心前方有没有坑；
  • Sarsa会比较顾及前方的坑位，所以会尽可能绕过坑位；

​ （在现实生活中可能倾向Sarsa，因为没有那么多机器人来掉坑）

Sarsa（lambda）

Sarsa->Sarsa（lambda）是从单步更新转为局部更新（回合更新）。

lambda理解为局部搜索的权重值，离宝藏越近局部搜索越激烈

伪代码

代码：

eligibility_trace：表示每个状态后选择相同动作几次（插旗子），当长时间没有获得reward会逐渐衰减，直到为0；

Sarsa(lambda)：

  • self.eligibility_trace.loc[s, :] *= 0；self.eligibility_trace.loc[s, a] = 1：对于经历过的 state-action, 我们让他+1, 证明他是得到 reward 路途中不可或缺的一环
  • self.eligibility_trace *= self.gamma*self.lambda_：随着时间衰减 eligibility trace 的值, 离获取 reward 越远的步, 他的"不可或缺性"越小
  • 在每一回合结束之后需要RL.eligibility_trace *= 0：eligibility trace 只是记录每个回合的每一步, 新回合开始的时候需要将 Trace 清零
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class SarsaLambdaTable(RL):
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9, trace_decay=0.9):
        super(SarsaLambdaTable, self).__init__(actions, learning_rate, reward_decay, e_greedy)

        # backward view, eligibility trace.
        self.lambda_ = trace_decay
        self.eligibility_trace = self.q_table.copy()

    def check_state_exist(self, state):
        if state not in self.q_table.index:
            # append new state to q table
            to_be_append = pd.Series(
                    [0] * len(self.actions),
                    index=self.q_table.columns,
                    name=state,
                )
            self.q_table = self.q_table.append(to_be_append)

            # also update eligibility trace
            self.eligibility_trace = self.eligibility_trace.append(to_be_append)

    def learn(self, s, a, r, s_, a_):
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, a_]  # next state is not terminal
        else:
            q_target = r  # next state is terminal
        error = q_target - q_predict

        # increase trace amount for visited state-action pair

        # Method 1（无封顶）:
        # self.eligibility_trace.loc[s, a] += 1

        # Method 2（有封顶）:
        self.eligibility_trace.loc[s, :] *= 0
        self.eligibility_trace.loc[s, a] = 1

        # Q update
        self.q_table += self.lr * error * self.eligibility_trace

        # decay eligibility trace after update
        self.eligibility_trace *= self.gamma*self.lambda_

**总结：**每步完成后都会更新全体的Q表，但是每次更新完Q表后都对当前的eligibility乘了一个衰减因子lambda，这里就和sarsa(lambda)思想一致了，因为不止有下一步会影响这一步，对于后面的所有步都对当前步有影响，但是随着步数的增加，后续步数对当前步的影响会衰减，衰减速率和lambda的取值有关。

DQN

实际上是一种Q-Learning方法，但是结合上了神经网络。如果只是单纯的结合神经网络去分析observation或者state，可能会有难收敛的毛病。

​ 但是DQN用了两种方式：记忆库（用于重复学习）和暂时冻结q_target参数（切断相关性）。

  • 记忆库用来存储各种记忆，之后再离散或者随机的调用之前存储好的记忆这种切断相关性的方法可以让神经网络更有效率的学习；
  • 暂时冻结q_target参数：q现实当中可以暂时冻结神经网络的一些参数，使他是一个短期之内没有被更新的参数；q估计是每走一步就更新一次参数（可能过了几千步的样子，再将q估计的参数同步赋值给q_target参数）

伪代码

代码：

  • q_eval = self.eval_net(state).gather(1, action):当达到一定步数时，获取记忆库中s所获取的下一步动作（已经在记忆库中随机抽出batch_size个样本）——估计Q值；
  • q_next = self.target_net(next_state).detach()：按照记忆库中的s_计算出新的a’的Q值——真实Q值；
  • q_target = reward + self.gamma * q_next.max(1)[0].unsqueeze(1)：参考伪代码的$y_i$（这里的q_next.max对应代码其实就是最大误差）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def learn(self):
    # print("<learn>")
    # 到达一定步数将Q网络的参数复制到目标网络
    if self.learn_step_counter % self.replace_target_iter == 0:
        self.target_net.load_state_dict((self.eval_net.state_dict()))
        # print('target_params_replaced')
    self.learn_step_counter += 1

    # 使用记忆库中批量数据
    if self.memory_counter < self.memory_size:
        sample_index = np.random.choice(self.memory_counter, self.batch_size)
    else:
        sample_index = np.random.choice(self.memory_size, self.batch_size)  # 2000个中随机抽取48个作为batch_size
    memory = self.memory[sample_index, :]  # 抽取的记忆单元，并逐个提取
    state = torch.FloatTensor(memory[:, :2])    # 第1，2列(x,y)坐标
    action = torch.LongTensor(memory[:, 2:3])   # 第3列
    reward = torch.LongTensor(memory[:, 3:4])   # 第4列
    next_state = torch.FloatTensor(memory[:, 4:6])  # 第5，6列(x,y)坐标

    # 计算loss
    # q_eval:存储估测值
    # q_next:按照target_net网络（隔一段时间更新参数）算出真实值
    q_eval = self.eval_net(state).gather(1, action)     # eval_net->(64,4)->按照action索引提取出q_value
    q_next = self.target_net(next_state).detach()

    # torch.max->[values=[],indices=[]] max(1)[0]->values=[]
    q_target = reward + self.gamma * q_next.max(1)[0].unsqueeze(1)     # label
    loss = self.loss(q_eval, q_target)
    self.cost.append(loss)
    # 反向传播更新
    self.optimizer.zero_grad()  # 梯度重置
    loss.backward()  # 反向求导
    self.optimizer.step()  # 更新模型参数

总结：DQN就是在Q-Learning中把获取Q值的Tabel换成了神经网络，除此之外引入记忆库和双神经网络。在达到一定步数之后， T网络（参数暂时不变）作为估测Q值（获取来源时一直在更新的memory，随机获取memory里面的）， Q网络作为真实Q值，求出相互之间的Loss，反向传播更新 Q网络的参数，达到一定要求之后将 Q网络的参数赋给 T网络。

Double DQN和DQN的区别

DQN 的神经网络部分可以看成一个 最新的神经网络 + 老神经网络, 他们有相同的结构, 但内部的参数更新却有时差. 而它的 Q现实 部分是这样的

因为我们的神经网络预测 Qmax 本来就有误差, 每次也向着最大误差的 Q现实 改进神经网络, 就是因为这个 Qmax 导致了 overestimate. 所以 Double DQN 的想法就是引入另一个神经网络来打消一些最大误差的影响. 而 DQN 中本来就有两个神经网络, 我们何不利用一下这个地理优势呢。所以, 我们用 Q估计 的神经网络估计 Q现实 中 Qmax(s’, a’) 的最大动作值. 然后用这个被 Q估计 估计出来的动作来选择 Q现实 中的 Q(s’)。

总结一下：有两个神经网络: Q_eval (Q估计中的), Q_next (Q现实中的)。

原本的 Q_next = max(Q_next(s’, a_all))在Double DQN中的 Q_next = Q_next(s’, argmax(Q_eval(s’, a_all)))，也可以表达成下面那样：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def learn(self):
    # check to replace target parameters
    if self.learn_step_counter % self.replace_target_iter == 0:
        self.target_net.load_state_dict((self.eval_net.state_dict()))
        print('\ntarget_params_replaced\n')

    if self.memory_counter > self.memory_size:
        sample_index = np.random.choice(self.memory_size, size=self.batch_size)
    else:
        sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
    batch_memory = self.memory[sample_index, :]

    state = torch.FloatTensor(batch_memory[:, :self.n_features])
    action = torch.LongTensor(batch_memory[:, self.n_features:self.n_features+1])
    reward = torch.LongTensor(batch_memory[:, self.n_features+1:self.n_features + 2])
    next_state = torch.FloatTensor(batch_memory[:, -self.n_features:])

    q_eval = self.eval_net(state).gather(1, action)  # eval_net->(64,4)->按照action索引提取出q_value

    if self.double_q:
        # 使用一直在更新的Q网络求出应该选择的下一state的动作
        max_action = self.eval_net(next_state).max(1)[1].view(-1, 1)
        # 使用隔段时间才更新的T网络求出根据Q网络算出的动作的Q值
        max_next_q_values = self.target_net(next_state).gather(1, max_action)
    else:
        # 原DQN，直接用T网络求出下一state的最大Q值
        max_next_q_values = self.target_net(next_state).max(1)[0].view(-1, 1)    # the natural DQN

    q_target = reward + self.gamma * max_next_q_values

    loss = self.loss(q_eval, q_target)
    self.cost_his.append(loss)
    # 反向传播更新
    self.optimizer.zero_grad()  # 梯度重置
    loss.backward()  # 反向求导
    self.optimizer.step()  # 更新模型参数

    self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_max
    self.learn_step_counter += 1

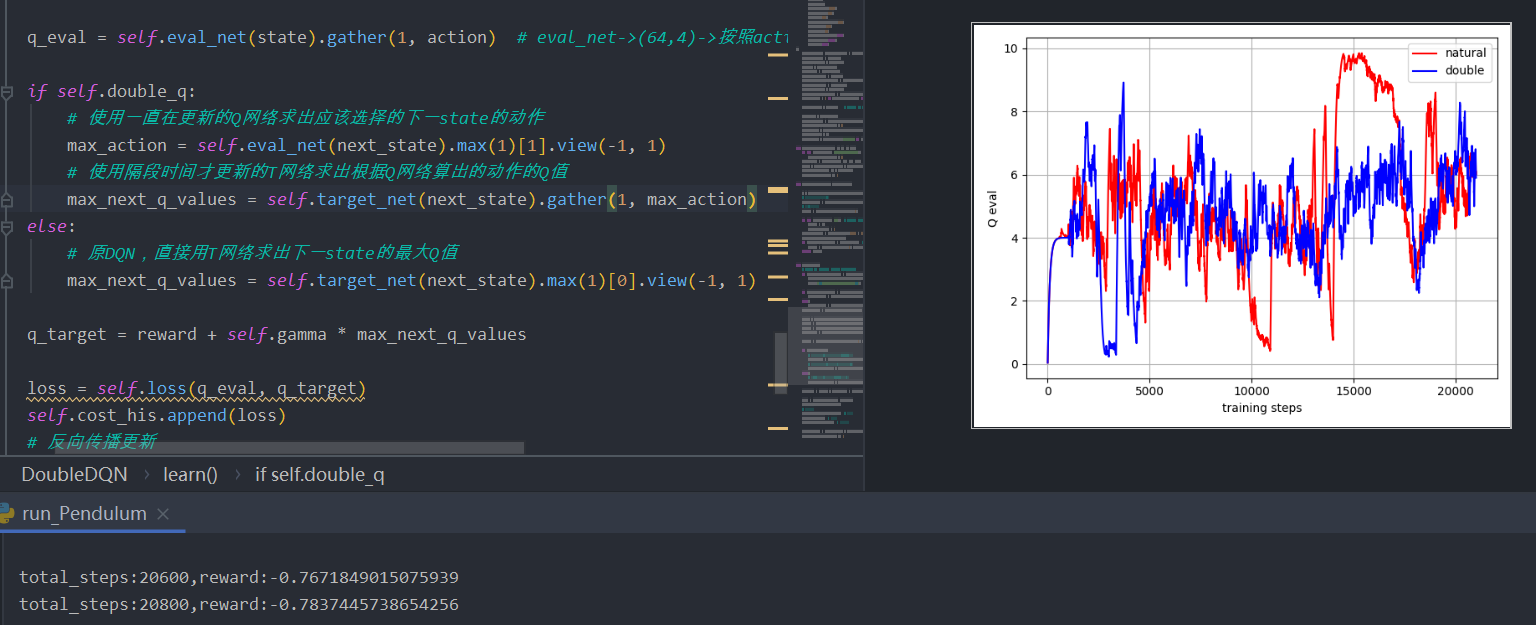
二者之间在代码中的最大区别在于以下代码

DDQN：

  • max_action = self.eval_net(next_state).max(1)[1].view(-1, 1)：使用一直在更新的Q网络求出应该选择的下一state的动作
  • max_next_q_values = self.target_net(next_state).gather(1, max_action)：使用隔段时间才更新的T网络求出根据Q网络算出的动作的Q值

DQN：

  • max_next_q_values = self.target_net(next_state).max(1)[0].view(-1, 1)：原DQN，直接用T网络求出下一state的最大Q值

总结：

  1. DQN在计算真实值时，使用的神经网络是q_target，该网络隔一段时间才会更新参数，计算出来的Q值其实是选出来的最大损失值（但实际上会有误差），但调参的目的就是为了loss越来越小；
  2. DDQN因此在计算Q值（损失）这一步再加入一个神经网络，先用Q网络（一直在更新）算出应该选择的action，再由T网络（隔一段时间更新）计算该action的Q值（损失）
  3. 理解上DDQN就是为了加快DQN的收敛速度所提出来的