强化学习之马尔科夫知识
马尔可夫过程
State
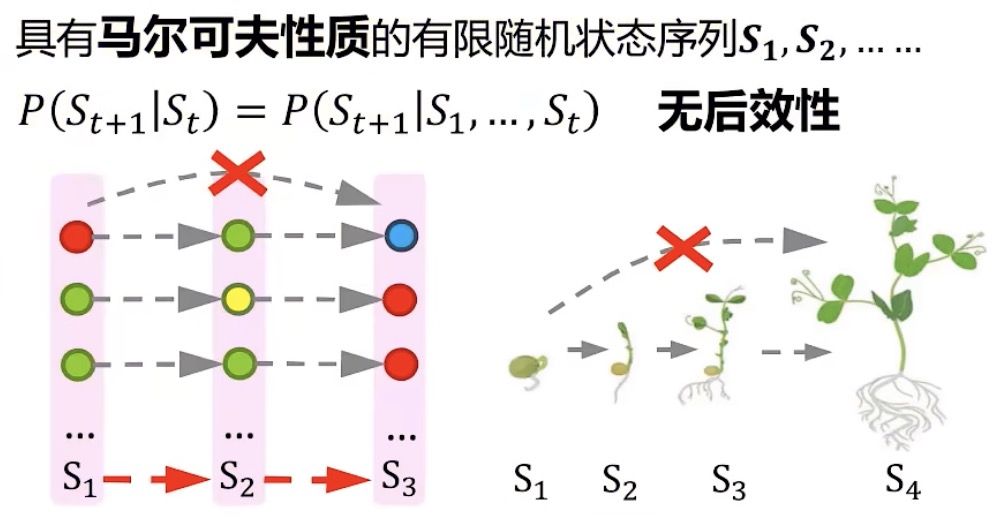
马尔科夫性质
无后效性:当前状态仅由上一状态决定,并不能由上上层状态影响,即层层影响。S2蕴含 S1的作用体系,S3蕴含S1和S2的作用体系…
Probability
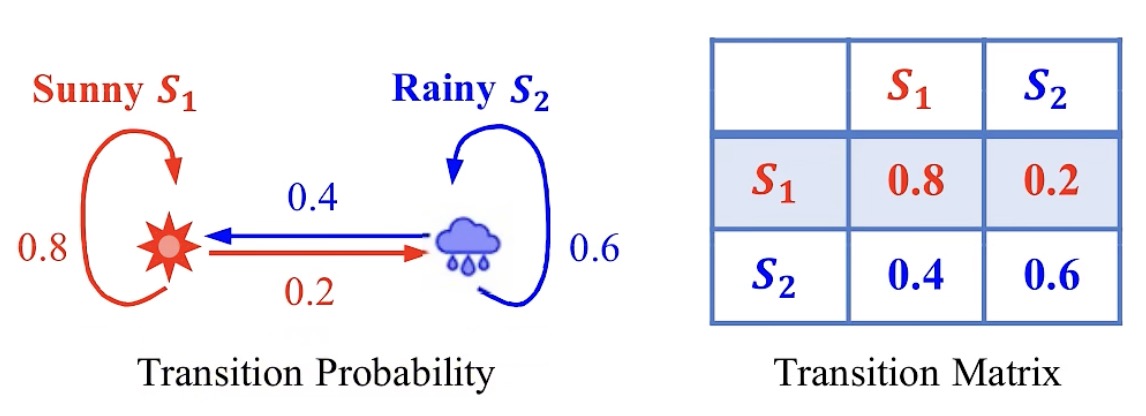
转移概率(下图左):今天是Sunny,第二天还是Sunny的概率是0.8,第二天是Rainy的概率是0.2;今天是Rainy,第二天还是Rainy的概率是0.6,第二天是Sunny的概率是0.4
转移矩阵(下图右)
状态(State)+ 状态转移概率(Probability) = 马尔可夫过程
隐马尔可夫过程
情景:疫情期间被隔离,看不到外面的天气,只能从医护人员的表情中猜测天气
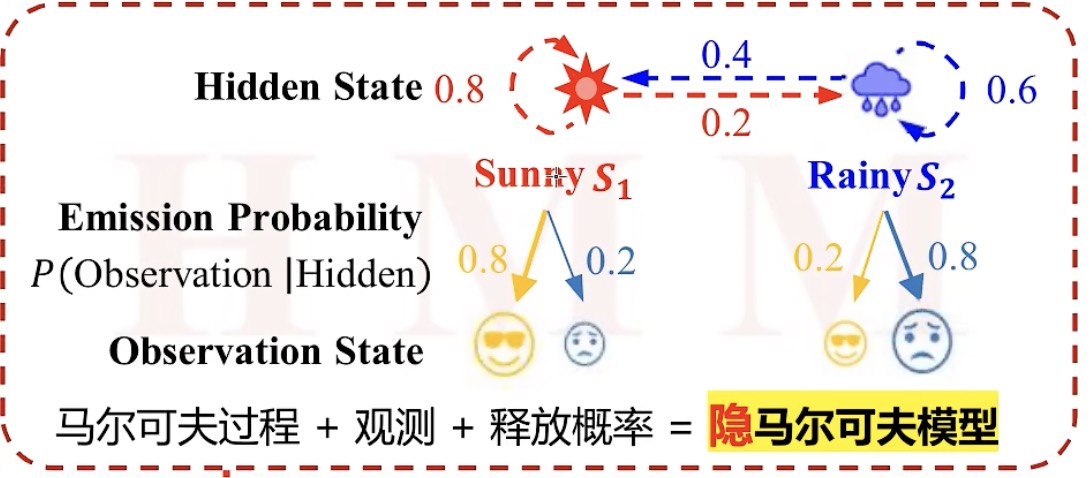
观察状态(Observation State):医护人员的表情,开心、伤心
释放概率(Emission Probability):如果今天是Sunny,那么医护人员有0.8概率是高兴的,有0.2概率是伤心;如果今天是Rainy,医护人员有0.2的概率是开心,0.8的概率是伤心。其中的0.8、0.2即释放概率,是一个条件概率P(Observation|Hidden)
应用(知二求一)
- 评估问题:已知天气为Sunny、Sunny、Rainy和释放概率0.8、0.2这样的情况,求解医护人员可能性最大的表情构成序列的是什么样子的。
- 解码问题:已知医护人员的表情构成序列和释放概率0.8、0.2这样的情况,求解可能性最大的天气构成序列的是什么样子的
- 学习问题:已知天气序列和医护人员的表情构成序列,求解释放概率参数是什么样子的

马尔可夫奖励过程

马尔可夫决策过程
动作产生不确定的状态转移
不确定的来源:某状态的某动作,导致不同的状态转移
例如:小孩在玩的状态下突然拿起奶瓶,下一个状态可能是拿起奶瓶继续玩,也有可能拿起奶瓶吃,也有可能拿起奶瓶睡了

动态规划
动作产生确定的状态转移
当动作产生确定的状态转移时,就成了一个动态规划问题
例如:(把节点作为状态,路段作为动作)每个圆圈都是一个道路节点,每个连线都是一个连接节点的路段。如果再i节点选择了红色的路段,下一个状态一定会到红色路段对应的节点。
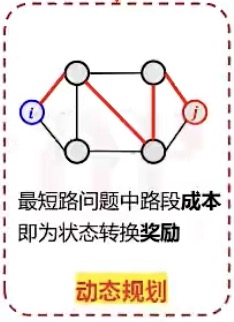
马尔科夫奖励过程
state+probability+reward
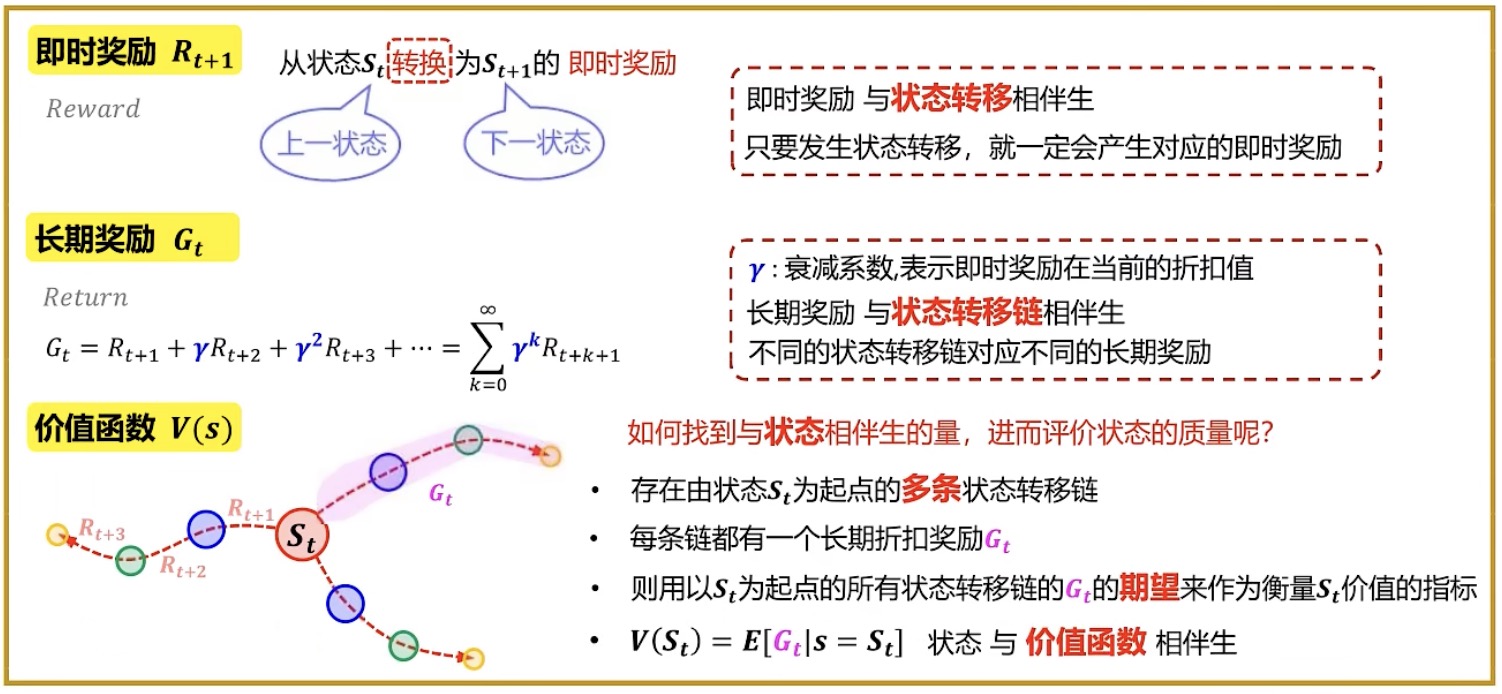
马尔可夫决策过程
state+probability+reward+action
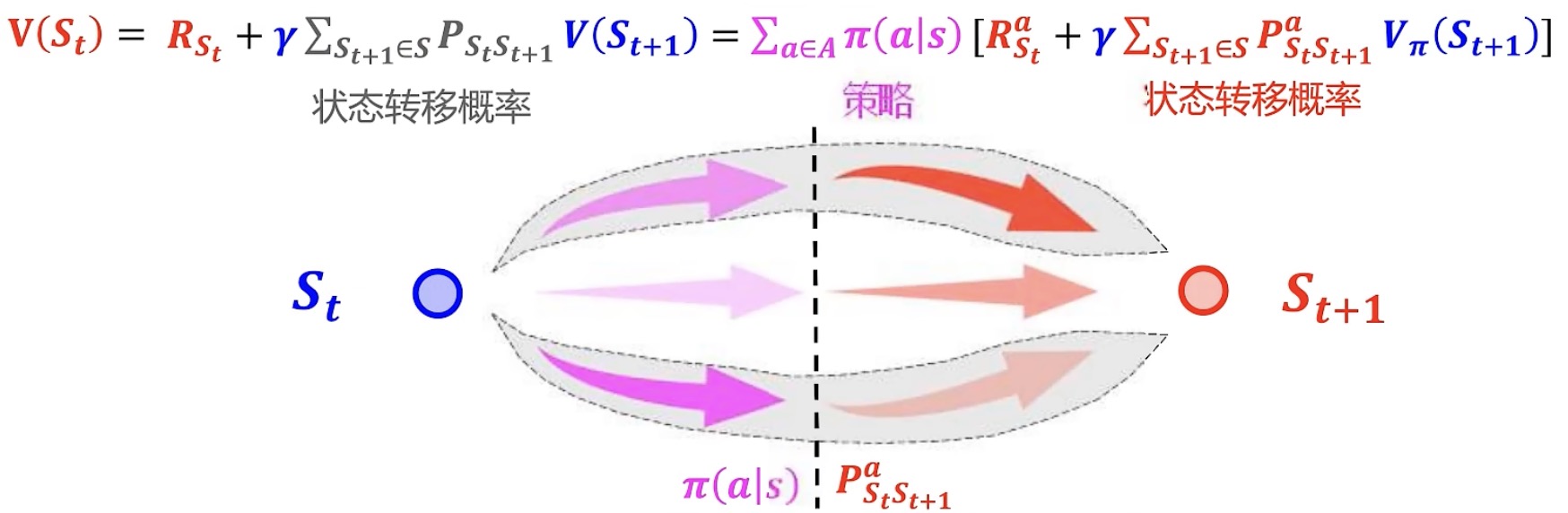
贝尔曼期望方程:将V(s)写成递归式,即贝尔曼期望方程
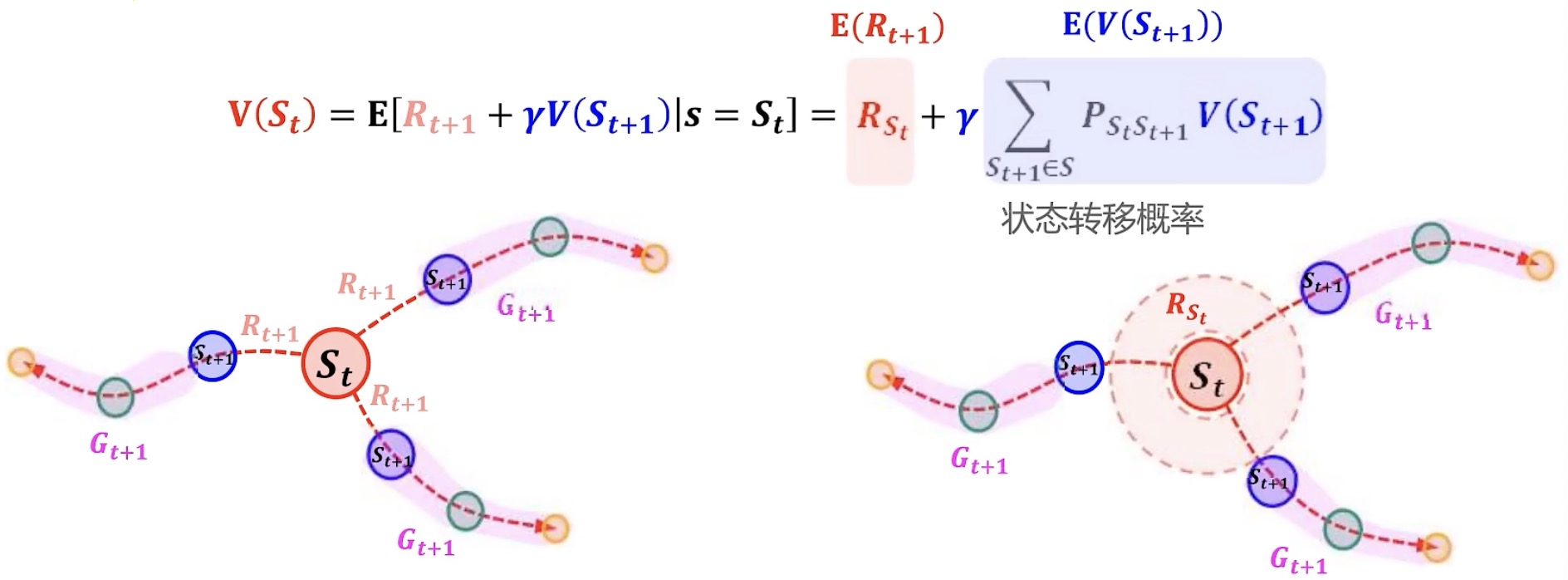
假设所有的$R_{t+1}$的期望等于$E(R_{t+1})$,$V(R_{t+1})$引入状态转移概率来加权。那么以下图左所示,$S_t$到底转移到哪一个$R_{t+1}$呢?按照状态转移概率进行选择。
因此引入状态转移概率作为权重,每条链子 X 转移到该条链子的可能性的和,就是期望
综上,从下图左——>下图右
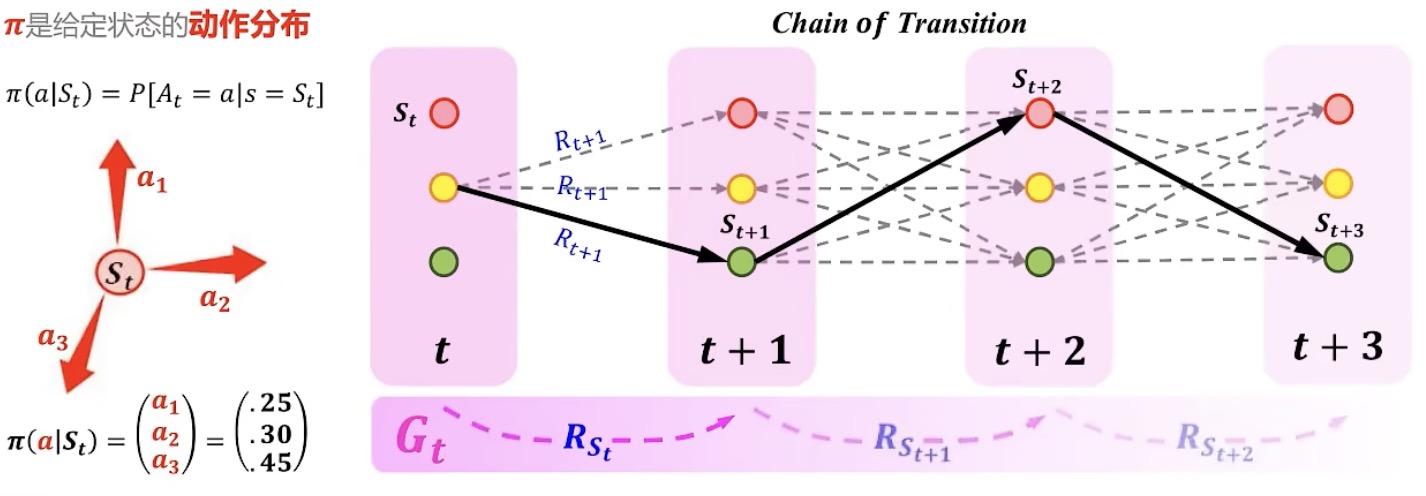
动作Action
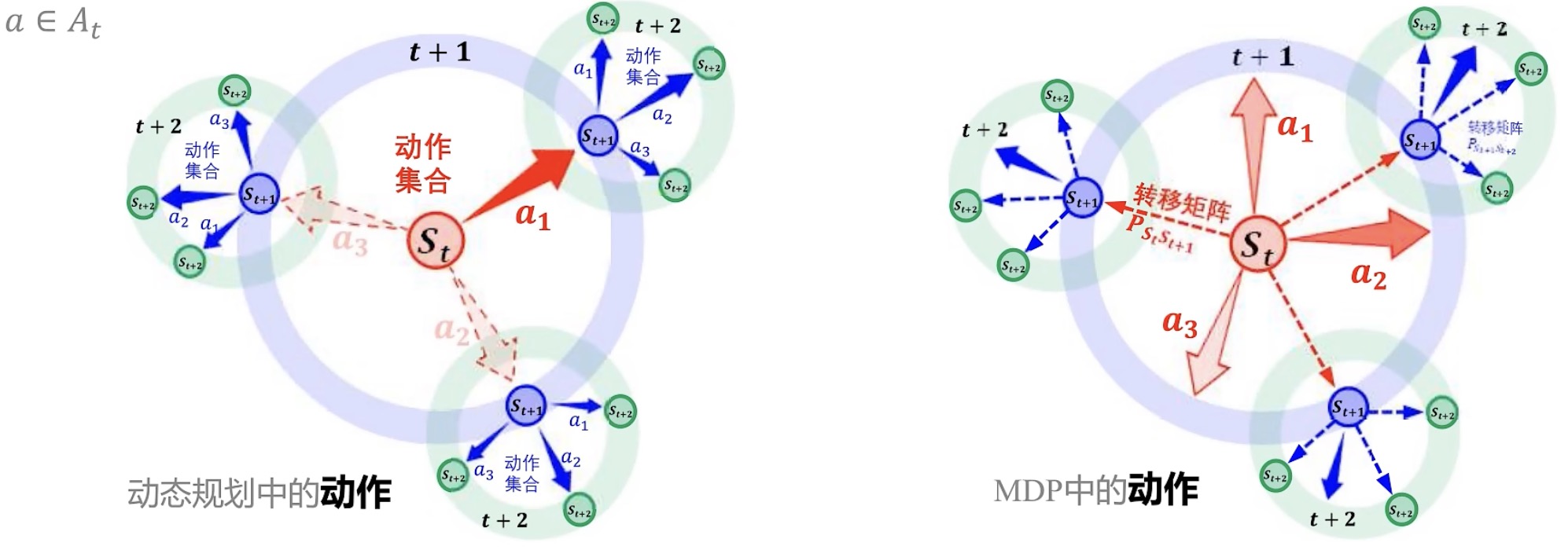
策略policy π(a|s):在某状态$S_t$下做某动作的概率分布
下图左,假设在$S_t$状态下能够有三种动作可能性,分别是25%、30%、45%,就是π。
在求解贝尔曼最优方程、贝尔曼期望方程,尤其是贝尔曼最优方程中,就是不断的找最好的π,让将25%、30%、45%坍缩成0,0,1的问题。
正是因为π影响产生一定的随机性,因此将其坍塌成确定性的问题。用贪婪的思想去得到最优策略(下图右),最终找到受益最大的一条链,反推回来。
贝尔曼期望方程的图形解释
通俗解释:将你爱我有几分的问题——>你爱不爱我的问题
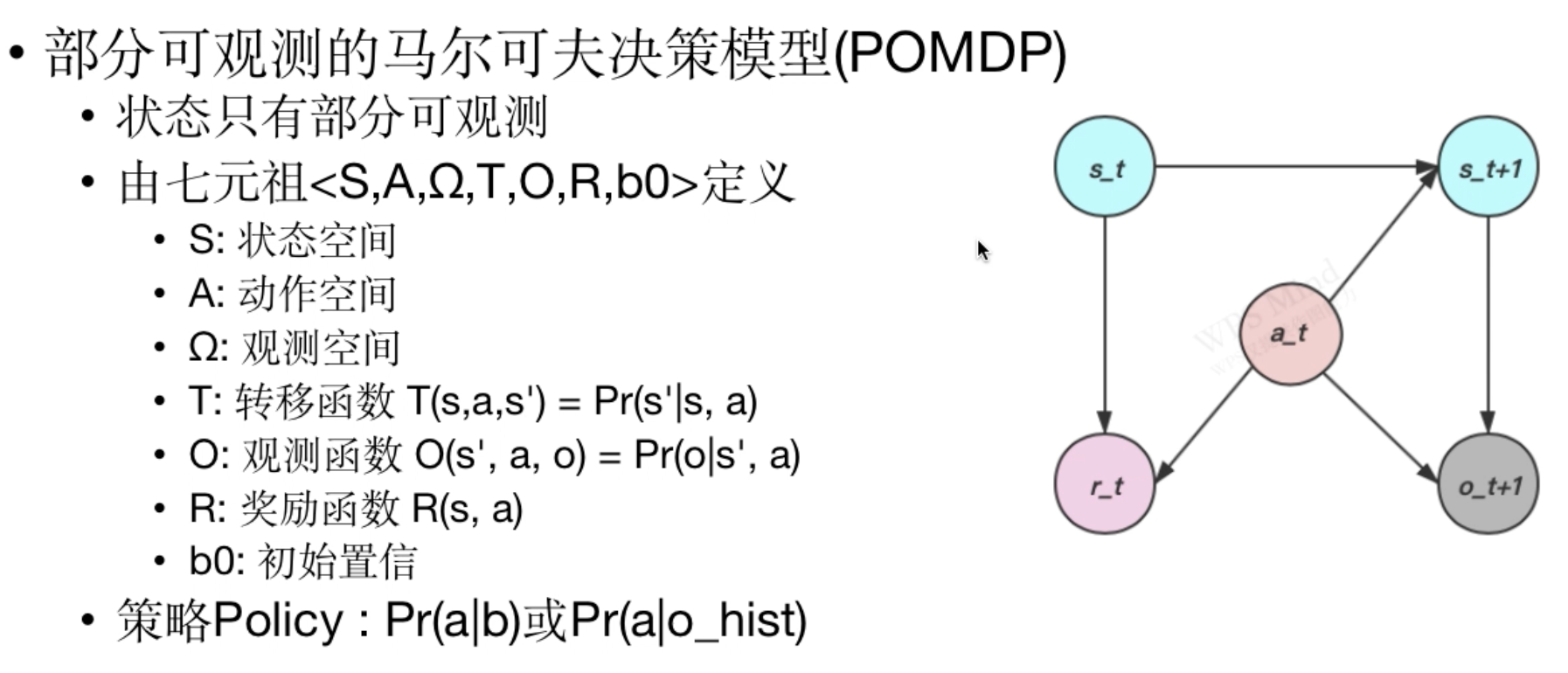
部分可观测马尔可夫决策过程*
Pr(a|b):在知道当前置信为b的情况下,选择动作a的概率
Pr(a|o_hist):在知道过去观察历史的情况下,选择动作a的概率