开学篇之图像分类评价指标

发表于 更新于 分类于 阅读次数： Valine： 本文字数： 7.9k 阅读时长 ≈ 7 分钟
主要学习图像分类中的评价指标，包括二分类和多分类任务下的指标含义。

分类指标

二分类：分类只有2个，如0，1分类；猫狗粉来；医学疾病的二分类（注：一般0、Neg代表正常/良性；1、Pos代表癌症/恶性）等

多分类：比较常见，例如imageNet-1000分类问题，CIFAR-10的10分类问题等。

二分类评价指标

Accuracy（准确率）、Precision（精确率）、Recall（召回率）、F1-Score、AUC、ROC、P-R曲线等

标签真实值 预测-正例 预测-负例
正例 真正例（A） TP 假负例（C） FN
负例 假正例（B） FP 真正例（D） TN

备注：T/F分别代表True/False，表示预测结果与标签是否一致；P/N分别代表Positives/Negatives，表示预测结果值属于正/负例。

  • A.True Positives，TP：预测为正，实际为正，预测为正样本是对的；
  • B.False Positives，FP：预测为正，实际为负，预测为正样本是错的；
  • C.False Negatives，FN：预测为负，实际为正，预测为负样本是错的；
  • D.True Negatives，TN：预测为负，实际为负，预测为负样本是对的。

Accuracy（准确率/精度）

——对于给定的数据，分类正确样本数占总样本数的比例。

$$Accuracy=\frac{TP+TN}{TP+TN+FN+FP}$$

缺陷：准确率这一指标在不平衡的数据集上的表现很差，因为如果正负样本数目差别很大（正例990个，负例10个），那么如果把样本全部预测为正例，计算得出的Acc为99%，即使表面上看Acc准确率很高，但实际上这个模型没有半点鬼用。

Precision（准确率/查准率）

——分类正确的正样本个数占分类器所有预测正样本个数的比例。即以判断为正例作为基准：模型判别为正例的里面，实际正确的概率是多少。

$$Precision=\frac{TP}{TP+FP}$$

题外话：个人感觉目前好像没发现该指标有什么不太好的地方，毕竟当预测时，如果有10正例，990负例，那么当模型不准确时，全预测为正例，那么准确率也才10%（以正例为基准），如果全预测为负例，那么也是0%。由此得出Precision在一定程度上是能表现出模型准确度的，但看那么多资料好像都不怎么评价该指标…（可能现在学的太浅，可能后续会知道吧）。

Recall（召回率/查全率）

分类正确的正样本个数占实际正样本个数的比例。以真实为正例作为基准：真实值的正例中，被判断出来正例的概率是多少。

$$Recall=\frac{TP}{TP+FN}$$

缺陷：假设有一样本（正例10，负例990），但是模型分类将所有样本都分为正例，即TP=10，FN=990，即此刻Recall = 100%，实际上目前模型依旧什么鬼用也没有。

F1-Score

为正确率和召回率的调和平均值，当数据集的类别个数不均衡时，或许是一个比单纯的Accuracy更好的指标。

$$F1-Score=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}=2·\frac{Precision·Recall}{Precision+Recall}$$

ROC(Receiver Operating Characteristic)

准确率、精准率、召回率和F1-Score都是单一的数值指标，如果想观察分类算法在不同的参数下的表现，可以使用ROC曲线。ROC曲线可以用评价一个分类器在不同阈值下的表现。横纵坐标均基于真实值为分母。

  • 横坐标是FPR（False Position Rate，假正率）：$\frac{FP}{N}=\frac{FP}{FP+TN}$，表示预测为正例但实际为负例的样本占所有负例样本（真实结果为负样本）的比例，FPR越大，预测正类中的实际负类就越多；
  • 纵坐标是TPR（True Position Rate，真正率）：$\frac{TP}{N}=\frac{TP}{TP+FN}$，表示预测为正例且实际为正例的样本占所有正例样本（真实结果为正样本）的比例。

补充：

  • TPR又称为召回率Recall、灵敏度Sensitivity，漏诊率=1-灵敏度；
  • 特异度Specifivity=1-FPR。

ROC曲线有四个关键点（曲线越靠近左上角效果越好）：

  • （0，0）：即FPR=TPR=0，即FP（False Positive）=TP（True Positive）=0，可以发现该分类器预测所有的样本都为负样本（Negative）；
  • （1，1）：即FPR=TPR=1，分类器实际上预测所有的样本都为正样本；
  • （0，1）：即FPR=0, TPR=1，这意味着FN（False Negative）=0，并且FP（False Positive）=0。意味着这是一个完美的分类器，它将所有的样本都正确分类；
  • （1，0）：即FPR=1，TPR=0，意味着这是一个糟糕的分类器，因为它成功避开了所有的正确答案。

ROC曲线图中，越靠近(0,1)的点对应的模型分类性能越好，所以，可以确定的是ROC曲线图中的点对应的模型，它们的不同之处仅仅是在分类时选用的阈值(Threshold)不同，每个点所选用的阈值都对应某个样本被预测为正类的概率值

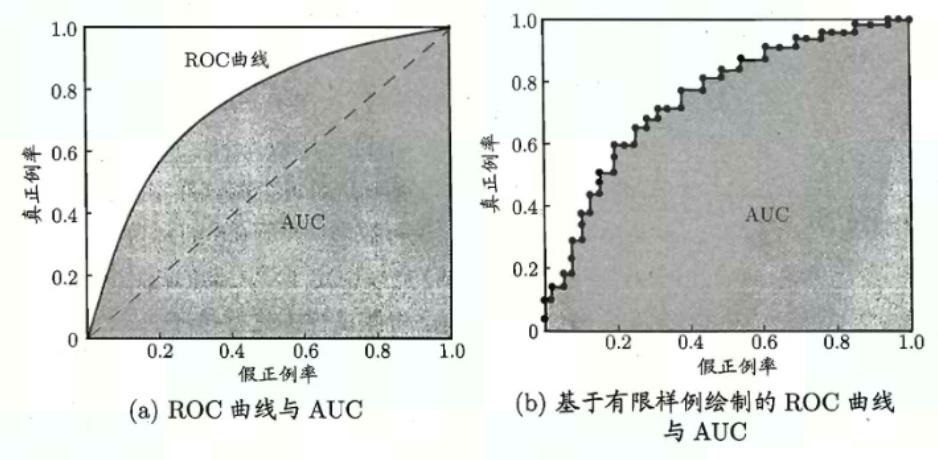
ROC曲线与AUC

ROC曲线有一个很好的特征：当测试集中的正负样本比例分布发生变化时，ROC曲线能够保持不变，即它对政府样本不均衡问题不敏感。所以对不均衡样本问题，通常选择ROC曲线作为评价标准；

ROC曲线越接近左上角，表示该分类器的性能越好，若一个分类器的ROC曲线完全包住了另一个分类器ROC曲线，那么可以判断前者的性能更好。

如何通过ROC曲线来判断模型好坏？

ROC曲线没有交点：ROC曲线越靠近（0，1），则效果越好

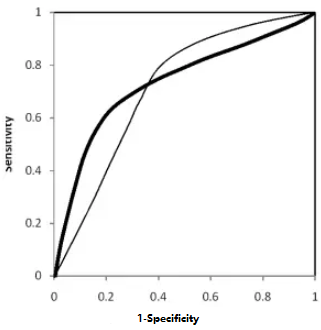
1-Specificity

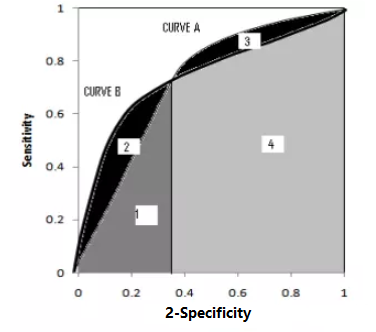
2-Specificity

ROC曲线有交点：模型A、B对应的ROC曲线相交却AUC值相等，此时就需要具体问题具体分析：当需要高Sensitivity值时，A模型好过B；当需要高Specificity值时，B模型好过A。

备注：

  • TPR又称为召回率Recall、灵敏度Sensitivity，漏诊率=1-灵敏度；
  • 特异度Specifivity=1-FPR。

AUC（Area Under Curve）

被定义为ROC曲线下与坐标轴围成的面积（如上图），显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。AUC越接近1.0，检测方法真实性越高;等于0.5时，则真实性最低，无应用价值。

  • AUC=1：在任何阈值下分类器都可以 100% 识别所有类别，这是理想的分类器；
  • AUC=0.5：相当于随机预测，此时分类器不可用；
  • 0.5<AUC<1：优于随机预测，这也是实际作用中大部分分类器所处的状态；
  • AUC<0.5：总是比随机预测更差；

AUC 作为一个评价标准，常和 ROC 曲线一起使用，可以看作是ROC的量化表现。

P-R曲线

以查准率（Precision）为纵轴、查全率（Recall）为横轴作图 ，就得到了查准率-查全率曲线，简称 “P-R曲线”。

P-R曲线

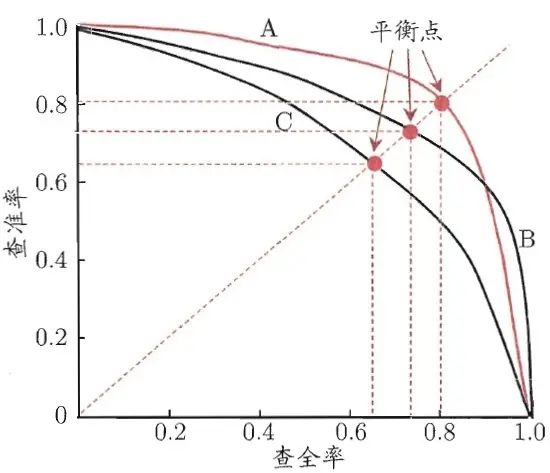
如何通过P-R曲线来判断模型好坏？

P-R曲线未发生交叉：即上图分类器A更优于分类器C，理解为可以将另一分类器在P-R图像上完全包住，可断言该分类器更优于被包住的分类器；

P-R曲线发生交叉：如上图分类器A和B，通常会引入平衡点（Break-Even Point，BEP）的概念，一个总和考虑查准率和查全率的性能度量（查准率==查全率时的取值）。基于BEP进行比较，可以认为上图分类器A比B效果更好。

AP（Average Precision）

就是Precision-Recall 曲线下围成的面积，通常来说一个越好的分类器，AP值越高。而mAP（mean average precision）是多个类别AP的平均值。

多分类评价指标

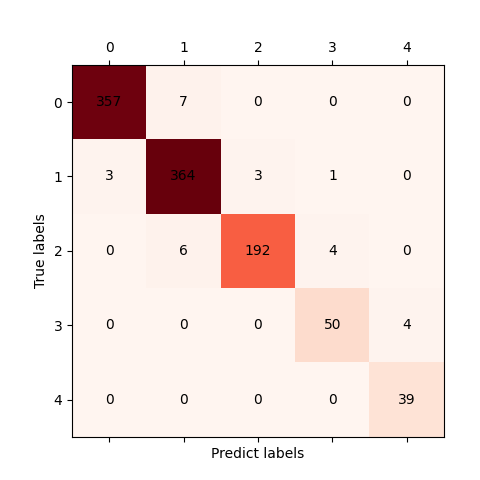
混淆矩阵（confusion matrix）

confusion matrix

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# eg：preds=[0,1,3,2,4,2,...],labels=[0,1,3,4,2,1,...]
# result()是自定义的预测相关函数，返回预测列表和所对应的真实label值列表
preds,labels = result()
C = confusion_matrix(labels, preds)
print(C)
# 图片对应的矩阵
# [[357   7   0   0   0]
#  [  3 364   3   1   0]
#  [  0   6 192   4   0]
#  [  0   0   0  50   4]
#  [  0   0   0   0  39]]
plt.matshow(C, cmap=plt.cm.Reds)

for i in range(len(C)):
    for j in range(len(C)):
        plt.annotate(C[j, i], xy=(i, j), horizontalalignment='center', verticalalignment='center')

plt.ylabel('True labels')
plt.xlabel('Predict labels')
plt.savefig(os.path.join(data2_path,"utils_images/confusion_matrix.png"))

Accuracy之top1和top5

在前面accuracy中已经有详细的解释（计算指定阈值的前k精度），这里把宏观上的公式展示出来

$$Acc-top1=\frac{第一个正确的个数和}{总数}$$

$$Acc-top5=\frac{前五之一正确的个数和}{总数}$$

1
2
3
4
5
6
7
8
9
10
11
12
13
labels = np.asarray([0,1,2,3])
preds = np.asarray([
    [0.7, 0.1, 0.1, 0.1],
    [0.1, 0.3, 0.4, 0.2],
    [0.3, 0.4, 0.2, 0.1],
    [0.0, 0.0, 0.1, 0.9]
])
accuracy = Accuracy(topk=(1, 2, 3))
print(accuracy(preds, labels))
# {'top1': 0.5, 'top2': 0.75, 'top3': 1.0}
accuracy = Accuracy(topk=2, thrs=(0.1, 0.5))
print(accuracy(preds, labels))
# {'top2_thr-0.10': 0.75, 'top2_thr-0.50': 0.5}
  • 对于Accuracy(topk=(1, 2, 3))，对应结果为top1、top2、top3，以top1和top3作为栗子。

top1即指精度为1，也就是在preds找出每一行中从大到小的第1个的index，栗子中即为[0，2，1，3]，top1就是求前者与labels=[0，1，2，3]的acuracy，即（1+0+0+1）/4=0.5；

top3即指精度为3，也就是在preds找出每一行中从大到小的前3名的index，栗子中即为[[0，1，2],[1，2，3],[，0，1，2],[0，2，3]]，top3就是求前者中每个向量（应该叫这个，就是列表里面的每一个列表）是否存在对应的label值，对应即为1，即（1+1+1+1）/4=1

  • 对于Accuracy(topk=2, thrs=(0.1, 0.5))，对应为top2_thr-0.10、top2_thr-0.50。

top2_thr-0.10即指在top2的前提下，对还剩余的值分别与thr的值（0.10）做对比。将preds中的每个预测值和thr对比，大于thr的设为1，小于等于thr的设为0。得到preds_new=[[1，0，0，0],[0，1，1，1],[1，1，1，0],[0，0，0，1]]；再根据topk=2，得到[[0，1],[1，2],[0，1],[0，3]]，所以（1+1+0+1）/4=0.75；

top2_thr-0.50即指在top2的前提下，对还剩余的值分别与thr的值（0.50）做对比。将preds中的每个预测值和thr对比，大于thr的设为1，小于等于thr的设为0。得到pred_new=[[1，0，0，0],[0，0，0，0],[0，0，0，0],[0，0，0，1]]；再根据topk=2，得到[[0，1],[0，1],[0，1],[0，3]]，所以（1+0+0+1）/4=0.5.

macro-F1

类比二分类指标，大体原则是每类计算对应指标，再求平均。其中每个类别的precision分别是对角线元素除以该元素所在的列元素之和；recall则是除以该类别所在行元素之和。

由上图图例confusion matrix所示，类别1的Precision_1=364/(7+364+6+0+0)=0.9655；Recall_1=364/(3+364+3+1+0)=0.9811。

计算方式（本处先对每类做R和R求平均，再代入F1；其他有是先对每类做F1，再求平均）：

1）对各类别对Precision的Recall求平均：

$$Precision_{macro}=\frac{\sum_{i=1}^nPrecision_i}{n}$$

$$Recall_{macro}=\frac{\sum_{i=1}^nRecall_i}{n}$$

2）然后利用F1计算公式计算出来的F1值即为Macro-F1:

$$F1_{macro}=\frac{2}{\frac{1}{macro_P}+\frac{1}{macro_R}}=2·\frac{Precision_{macro}·Recall_{macro}}{Precision_{macro}+Recall_{macro}}$$

简而言之：就是先对每一个类别的Precision和Recall分别求平均，得到平均的Precision和Recall，之后带入macro-F1的公式得到结果。

注意：因为对各类别的Precision和Recall求了平均，所以并没有考虑到数据数量的问题。在这种情况下，Precision和Recall较高的类别对F1的影响会较大。

micro-F1

与上面的macro不同，微查准查全，先将多个混淆矩阵的TP，FP，TN，FN对应位置求平均，然后按照Percision和Recall的公式求得micro-P和micro-R，最后根据micro-P和micro-R求得micro-F1。

计算方式：

1）先计算出所有类别的总的Precision和Recall：

$$Precision_{micro}=\frac{\sum_{i=1}^nTP_i}{\sum_{i=1}^nTP_i+\sum_{i=1}^nFN_i}$$

$$Recall_{micro}=\frac{\sum_{i=1}^nTP_i}{\sum_{i=1}^nTP_i+\sum_{i=1}^nFN_i}$$

2）利用F1计算公式计算出来的F1值即为Micro-F1:

$$F1_{micro}=2·\frac{Precision_{micro}·Recall_{micro}}{Precision_{micro}+Recall_{micro}}$$

简而言之：就是将每个类别的Precision和Recall做求和，再代入micro-F1公式中。

注意：因为其考虑了各种类别的数量，所以更适用于数据分布不平衡的情况。在这种情况下，数量较多的类别对F1的影响会较大。

mAP（mean Average Precision）

mAP（mean Accuracy Precision）一般而言，全类平均正确率（mAP，又称全类平均精度）是将所有类别的平均正确率（AP）进行综合加权平均而得到的。在目标检测领域使用更为普遍（目标检测那块再详细说明，因为暂时还没了解目标检测）。

$$mAP=\frac{1}{n}\sum(AP)_i$$

为什么要使用AP或者mAP？

我们希望一个模型的Precision和Recall都很高，所以需要综合考虑这两个因素，我们可以联想到用调和平均数F1-beta值来衡量，另一种方法正是PR曲线下的面积AUC，这也就是AP。AUC面积越接近1性能越好。曲线下的面积理解为不同召回值的情况下所有精度的平均值。

混淆矩阵kappa系数

使用在统计学中评估一致性的一种方法，取值范围[-1,1]，实际应用中，一般是[0,1]，与ROC曲线中一般不会出现下凸形曲线的原理类似。这个系数的值越高，则代表模型实现的分类准确度越高。基于混淆矩阵的kappa系数计算公式如下：

$$kappa=\frac{p_0-p_e}{1-p_e}$$

其中：

$p_0=\frac{对角线之和}{整个矩阵元素之和}$，也就是Accuracy

$p_e=\frac{\sum_i第i行元素和*第i列元素和}{(整个矩阵元素之和)^2}$

意义：根据kappa的计算公式，越不平衡的混淆矩阵，$p_e$越高，kappa的值就可能越低，正好能够给“偏向性”强的模型打低分，是一种能够惩罚模型的“偏向性”的指标来代替accuracy

1
2
from sklearn.metrics import cohen_kappa_score
kappa = cohen_kappa_score(y_true,y_pred，label=None) #(label除非是你想计算其中的分类子集的kappa系数，否则不需要设置)

性能指标（待补充）

机器性能FLOPS

  • OPS(Operations Per Second) ，每秒的操作次数

    • MOPS（Million Operation Per Second）：每秒钟可进行一百万次（10^6）操作

    • GOPS（Giga Operations Per Second）每秒钟可进行十亿次（10^9）操作

    • TOPS（Tera Operations Per Second）每秒钟可进行一万亿次（10^12）操作

    • POPS（peta Operations Per Second）每秒钟可进行一千万亿（=10^15）操作

  • FLOPS: (Floating Point operations per second), S大写， 指每秒浮点运算的次数，可以理解为运算的速度，是衡量硬件性能的一个指标。MFLOPS, GFLOPS, TFLOPS, PFLOPS 意义同上。

算法性能FLOPs

FLOPs：(Floating Point Operations) s小写，指浮点运算数，理解为计算量。可以用来衡量算法/模型的复杂度。（模型） 在论文中常用GFLOPs（1 GFLOPs = 10^9 FLOPs）。其它前缀单位意义同上。

一般计算FLOPs来衡量模型的复杂度，FLOPs越小时，表示模型所需计算量越小，运行起来时速度更快。

MAC(memory access cost, 内存访问成本)即存储该模型所需的存储空间。以卷积来举例：理解为卷积的总计算量需要访问内存，输出的结果需要存储，权重需要存储。也会被用来衡量模型的运行速度。

有一个基于pytorch的torch stat包，可以计算模型的FLOPs数，参数大小等指标

1
2
3
4
5
from torchstat import stat
import torchvision.models as models

model = model.alexnet()
stat(model, (3, 224, 224))