一些函数解释（更新ing）

发表于 更新于 分类于 阅读次数： Valine： 本文字数： 6.1k 阅读时长 ≈ 6 分钟
补充对于assert、torch.nn.Parameter() 、.item()、numpy.pad、torch.meshgrid、torch.stack函数的知识。

assert

用于程序调试

使用assert断言语句是一个非常好的习惯，python assert断言句语格式及用法很简单。在没完善一个程序之前，我们不知道程序在哪里会出错，与其让它在运行到最后崩溃，不如在出现错误条件时就崩溃，这样在跑大规模程序的时候不会过多的浪费时间和计算资源，这时候就需要assert断言的帮助。

例子1

1
assert expression

该形式用来测试断言的expression语句，如果expression是True，那么什么反应都没有。但是如果expression是False，那么会报错AssertionError。

如：

1
2
3
4
5
6
7
8
9
10
11
# 出错时
assert 1==0
---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-4-b09d6b060198> in <module>()
----> 1 assert 1==0,

AssertionError:
---------------------------------------------------------------------------
# 没有出错时什么也不反应
assert 1==1

例子2

1
assert expression1, expression2

assert断言语句可以添加异常参数，也就是在断言表达式后添加字符串信息，用来解释断言并更好的知道是哪里出了问题。格式如下：

1
2
assert expression [, arguments]
assert 表达式 [, 参数]

如：

1
2
3
4
5
6
7
8
9
10
11
# 出错时
assert 1==0, "出错了"
---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-4-b09d6b060198> in <module>()
----> 1 assert 1==0, "出错了"

AssertionError: 出错了
---------------------------------------------------------------------------
# 没有出错时依旧什么也不反应
assert 1==1, "出错了"

nn.Parameter()

parameter，中文意为参数。我们知道，使用PyTorch训练神经网络时，本质上就是训练一个函数，这个函数输入一个数据（如CV中输入一张图像），输出一个预测（如输出这张图像中的物体是属于什么类别）。而在我们给定这个函数的结构（如卷积、全连接等）之后，能学习的就是这个函数的参数了，我们设计一个损失函数，配合梯度下降法，使得我们学习到的函数（神经网络）能够尽量准确地完成预测任务。

通常，我们的参数都是一些常见的结构（卷积、全连接等）里面的计算参数。而当我们的网络有一些其他的设计时，会需要一些额外的参数同样很着整个网络的训练进行学习更新，最后得到最优的值，经典的例子有注意力机制中的权重参数、Vision Transformer中的class token和positional embedding等。

首先可以把这个函数理解为类型转换函数，将一个不可训练的类型Tensor转换成可以训练的类型parameter并将这个parameter绑定到这个module里面(net.parameter()中就有这个绑定的parameter，所以在参数优化的时候可以进行优化的)，所以经过类型转换这个self.v变成了模型的一部分，成为了模型中根据训练可以改动的参数了。使用这个函数的目的也是想让某些变量在学习的过程中不断的修改其值以达到最优化。

ViT中nn.Parameter()

在ViT中，positonal embedding和class token是两个需要随着网络训练学习的参数，但是它们又不属于FC、MLP、MSA等运算的参数，在这时，就可以用nn.Parameter()来将这个随机初始化的Tensor注册为可学习的参数Parameter。

1
2
3
4
...
self.pos_embedding = nn.Parameter(torch.randn(1, num_patches+1, dim))
self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
...

举个栗子

指定这两个参数的初始数值为0.98，并打印迭代器net.Parameters()。

1
2
3
4
...
self.pos_embedding = nn.Parameter(torch.ones(1, num_patches+1, dim) * 0.98)
self.cls_token = nn.Parameter(torch.ones(1, 1, dim) * 0.98)
...

实例化一个ViT模型并打印net.Parameters()：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
net_vit = ViT(
        image_size = 256,
        patch_size = 32,
        num_classes = 1000,
        dim = 1024,
        depth = 6,
        heads = 16,
        mlp_dim = 2048,
        dropout = 0.1,
        emb_dropout = 0.1
    )

for para in net_vit.parameters():
        print(para.data)

输出结果中可以看到，最前两行就是我们显式指定为0.98的两个参数pos_embedding和cls_token：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
tensor([[[0.9800, 0.9800, 0.9800,  ..., 0.9800, 0.9800, 0.9800],
         [0.9800, 0.9800, 0.9800,  ..., 0.9800, 0.9800, 0.9800],
         [0.9800, 0.9800, 0.9800,  ..., 0.9800, 0.9800, 0.9800],
         ...,
         [0.9800, 0.9800, 0.9800,  ..., 0.9800, 0.9800, 0.9800],
         [0.9800, 0.9800, 0.9800,  ..., 0.9800, 0.9800, 0.9800],
         [0.9800, 0.9800, 0.9800,  ..., 0.9800, 0.9800, 0.9800]]])
tensor([[[0.9800, 0.9800, 0.9800,  ..., 0.9800, 0.9800, 0.9800]]])
tensor([[-0.0026, -0.0064,  0.0111,  ...,  0.0091, -0.0041, -0.0060],
        [ 0.0003,  0.0115,  0.0059,  ..., -0.0052, -0.0056,  0.0010],
        [ 0.0079,  0.0016, -0.0094,  ...,  0.0174,  0.0065,  0.0001],
        ...,
        [-0.0110, -0.0137,  0.0102,  ...,  0.0145, -0.0105, -0.0167],
        [-0.0116, -0.0147,  0.0030,  ...,  0.0087,  0.0022,  0.0108],
        [-0.0079,  0.0033, -0.0087,  ..., -0.0174,  0.0103,  0.0021]])
...
...

这就可以确定nn.Parameter()添加的参数确实是被添加到了Parameters列表中，会被送入优化器中随训练一起学习更新。

.item()

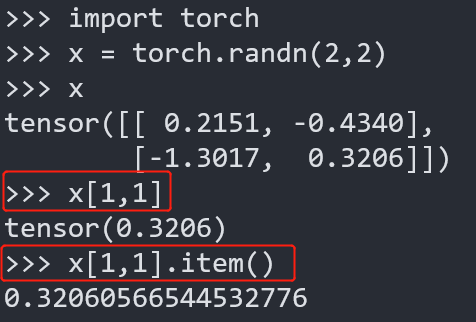
取出单元素张量的元素值并返回该值，保持原元素类型不变。,即：原张量元素为整形，则返回整形，原张量元素为浮点型则返回浮点型，etc

x[1,1] VS x.item():

1
2
3
4
5
6
7
import torch
x = torch.randn(2,2)
print(x)
# x[1,1]
print(x[1,1])
# x[1,1].item()
print(x[1,1].item())

.item()的作用

numpy.pad()

在卷积神经网络中，为了避免因为卷积运算导致输出图像缩小和图像边缘信息丢失，常常采用图像边缘填充技术，即在图像四周边缘填充0，使得卷积运算后图像大小不会缩小，同时也不会丢失边缘和角落的信息。在Python的numpy库中，常常采用numpy.pad()进行填充操作。

*numpy.pad(array, pad_width, mode=‘constant’, *kwargs)

array

表示需要填充的数组。

pad_width

表示每个轴（axis）边缘需要填充的数值数目。

参数输入方式为：（(before_1, after_1), … (before_N, after_N)），其中(before_1, after_1)表示第1轴两边缘分别填充before_1个和after_1个数值。

mode

表示填充的方式（取值：str字符串或用户提供的函数），总共有12种填充模式。

默认为’constant’方式填充。

**kwargs

表示关键字参数，它本质上是一个dict。

  1. constant_values : sequence or scalar, optional。用于‘constant’填充方式指定的填充值。
  2. stat_length : sequence or int, optional。用于 ‘maximum’, ‘mean’, ‘median’,和‘minimum’填充方式中。每个轴边缘用于计算统计量的数据个数，默认用到整个轴。
  3. end_values : sequence or scalar, optional。用于 ‘linear_ramp’填充方式，设定结束值。
  4. reflect_type : {‘even’, ‘odd’}, optional，默认为‘even’。

Swin Transformer中需要对输入图片进行padding处理

1
2
3
4
5
6
7
pad_input = (H % self.patch_size[0] != 0) or (W % self.patch_size[1] != 0)
if pad_input:
    # to pad the last 3 dimensions,
    # (W_left, W_right, H_top,H_bottom, C_front, C_back)
    x = F.pad(x, (0, self.patch_size[1] - W % self.patch_size[1],
                  0, self.patch_size[0] - H % self.patch_size[0],
                  0, 0))

torch.meshgrid（）

torch.meshgrid（）的功能是生成网格，可以用于生成坐标。函数输入两个数据类型相同的一维张量，两个输出张量的行数为第一个输入张量的元素个数，列数为第二个输入张量的元素个数，当两个输入张量数据类型不同或维度不是一维时会报错。

其中第一个输出张量填充第一个输入张量中的元素，各行元素相同；第二个输出张量填充第二个输入张量中的元素各列元素相同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 【1】
import torch
a = torch.tensor([1, 2, 3, 4])
print(a)
b = torch.tensor([4, 5, 6])
print(b)
x, y = torch.meshgrid(a, b)
print(x)
print(y)
 
结果显示：
tensor([1, 2, 3, 4])
tensor([4, 5, 6])
tensor([[1, 1, 1],
        [2, 2, 2],
        [3, 3, 3],
        [4, 4, 4]])
tensor([[4, 5, 6],
        [4, 5, 6],
        [4, 5, 6],
        [4, 5, 6]])
 
 
# 【2】
import torch
a = torch.tensor([1, 2, 3, 4, 5, 6])
print(a)
b = torch.tensor([7, 8, 9, 10])
print(b)
x, y = torch.meshgrid(a, b)
print(x)
print(y)
 
结果显示：
tensor([1, 2, 3, 4, 5, 6])
tensor([ 7,  8,  9, 10])
tensor([[1, 1, 1, 1],
        [2, 2, 2, 2],
        [3, 3, 3, 3],
        [4, 4, 4, 4],
        [5, 5, 5, 5],
        [6, 6, 6, 6]])
tensor([[ 7,  8,  9, 10],
        [ 7,  8,  9, 10],
        [ 7,  8,  9, 10],
        [ 7,  8,  9, 10],
        [ 7,  8,  9, 10],
        [ 7,  8,  9, 10]])

torch.stack（）

stack（tensors,dim=0,out=None）在维度上连接（concatenate）若干个张量。(这些张量形状相同）。

将若干个张量在dim维度上连接,生成一个扩维的张量，比如说原来你有若干个2维张量，连接可以得到一个3维的张量。

设待连接张量维度为n，dim取值范围为-n-1~n，这里得提一下为负的意义：-i为倒数第i个维度。举个例子，对于2维的待连接张量，-1维即3维，-2维即2维。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
a=torch.tensor([[1,2,3],[4,5,6]])
b=torch.tensor([[10,20,30],[40,50,60]])
c=torch.tensor([[100,200,300],[400,500,600]])
print(torch.stack([a,b,c],dim=0))
print(torch.stack([a,b,c],dim=1))
print(torch.stack([a,b,c],dim=2))
print(torch.stack([a,b,c],dim=0).size())
print(torch.stack([a,b,c],dim=1).size())
print(torch.stack([a,b,c],dim=2).size())
#输出结果为：
tensor([[[  1,   2,   3],
         [  4,   5,   6]],

        [[ 10,  20,  30],
         [ 40,  50,  60]],

        [[100, 200, 300],
         [400, 500, 600]]])
tensor([[[  1,   2,   3],
         [ 10,  20,  30],
         [100, 200, 300]],

        [[  4,   5,   6],
         [ 40,  50,  60],
         [400, 500, 600]]])
tensor([[[  1,  10, 100],
         [  2,  20, 200],
         [  3,  30, 300]],

        [[  4,  40, 400],
         [  5,  50, 500],
         [  6,  60, 600]]])
torch.Size([3, 2, 3])
torch.Size([2, 3, 3])
torch.Size([2, 3, 3])