Transformer中Self-Attention以及Multi-Head Attention详解

前言

Transformer是2017年Google在Computation and Language上发表的，当时主要是针对自然语言处理领域提出的（之前的RNN模型记忆长度有限且无法并行化，只有计算完$t_i$时刻后的数据才能计算$t_{i+1}$时刻的数据，但Transformer都可以做到）。在这篇文章中作者提出了Self-Attention的概念，然后在此基础上提出Multi-Head Attention，所以本文对Self-Attention以及Multi-Head Attention的理论进行学习。原论文：Attention Is All You Need

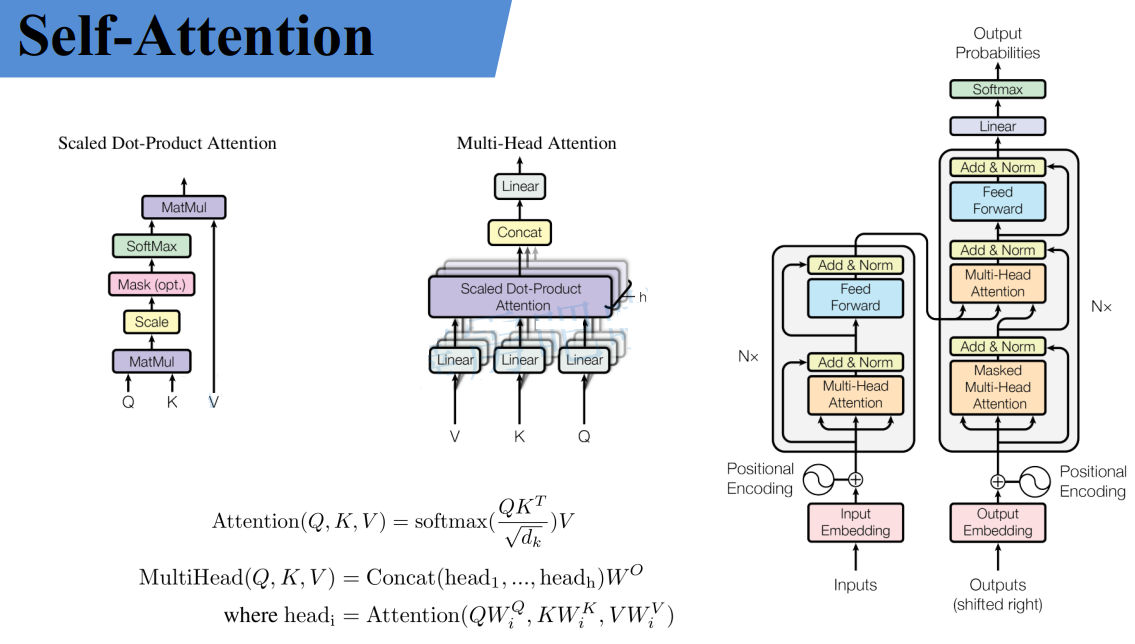
Self-Attention

假设输入的序列长度为2，输入就两个节点$x_1$，$x_2$，然后通过Input Embedding也就是图中的f(x)将输入映射到$a_1$，$a_2$。紧接着分别将$a_1$，$a_2$分别通过三个变换矩阵$W_q$，$W_k$，$W_v$（这三个参数是可训练的，是共享的）得到对应的$q^i$，$k^i$，$v^i$（这里在源码中是直接使用全连接层实现的，这里为了方便理解，忽略偏执）。

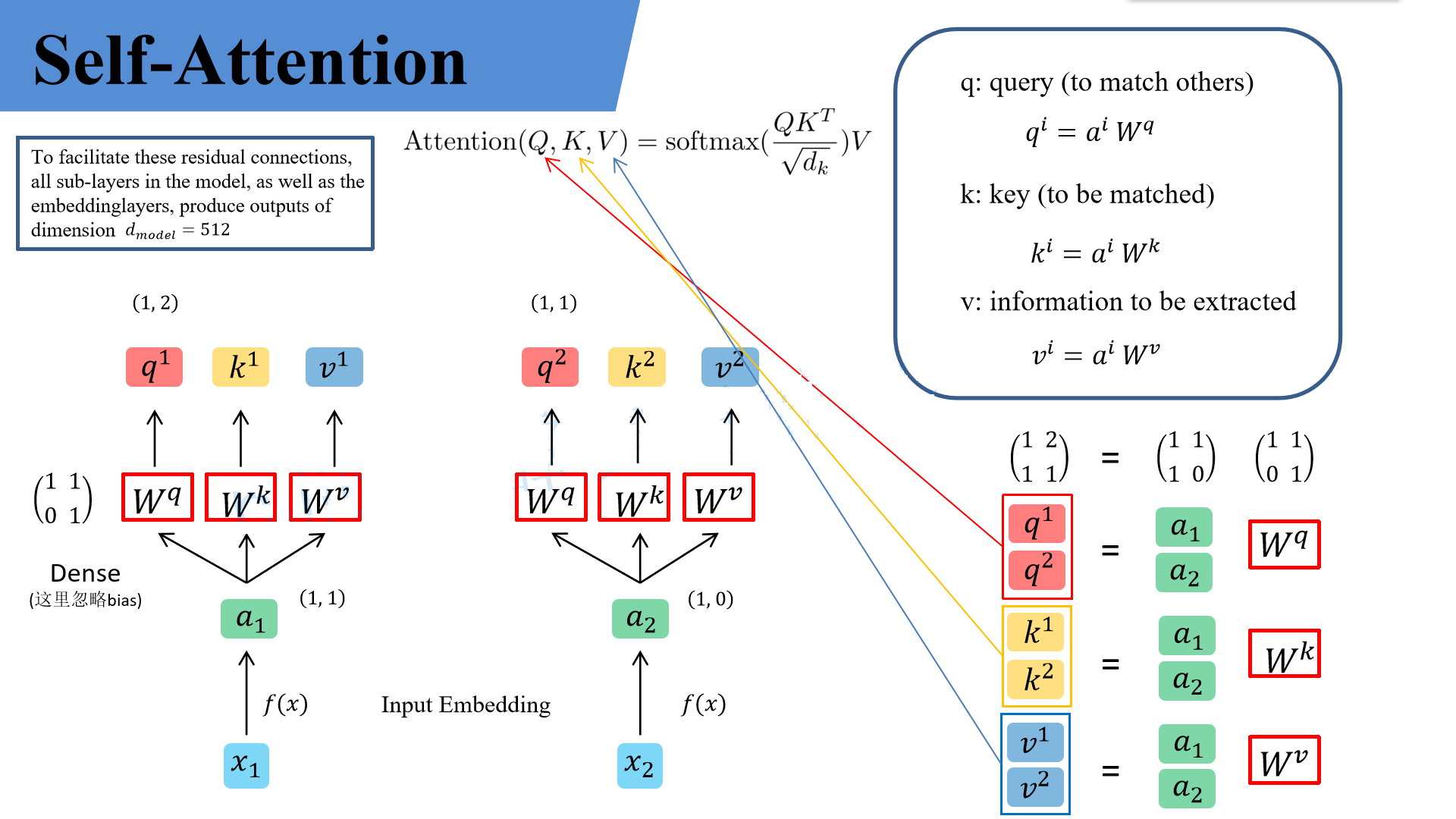
• $q$代表query，后续会去和每一个$k$进行匹配
• $k$代表key，后续会被每个$q$匹配
• $v$代表从$a$中提取得到的信息
• 后续$q$和$k$匹配的过程可以理解成计算两者的相关性，相关性越大对应$v$的权重也就越大

假设$a_1=(1，1)$，$a_2=(1，0)$，$W_q=\left(\begin{matrix} 1 & 1\\ 0 & 1\end{matrix}\right)$，那么：$$q^1=(1，1)\left(\begin{matrix} 1 & 1\\ 0 & 1\end{matrix}\right)=(1，2),\quad q^2=(1，0)\left(\begin{matrix} 1 & 1\\ 0 & 1\end{matrix}\right)=(1，1)$$

前面有说Transformer是可以并行化的，所以可以直接写成：$$\left(\begin{matrix} q^1\\ q^2\end{matrix}\right)=\left(\begin{matrix} 1 & 1\\ 1 & 0\end{matrix}\right)\left(\begin{matrix} 1 & 1\\ 0 & 1\end{matrix}\right)=\left(\begin{matrix} 1 & 2\\ 1 & 1\end{matrix}\right)$$

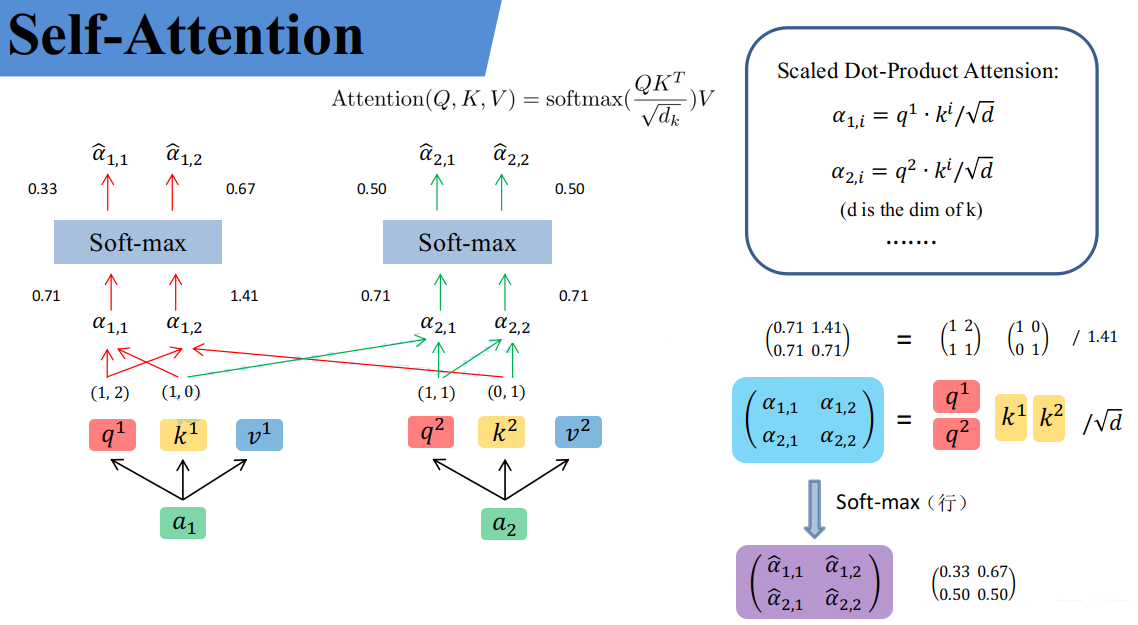
同理我们可以得到$\left(\begin{matrix} k^1\\ k^2\end{matrix}\right)$和$\left(\begin{matrix} v^1\\ v^2\end{matrix}\right)$，那么求得的$\left(\begin{matrix} q^1\\ q^2\end{matrix}\right)$就是原论文中的$Q$，$\left(\begin{matrix} k^1\\ k^2\end{matrix}\right)$就是$K$，$\left(\begin{matrix} v^1\\ v^2\end{matrix}\right)$就是$V$。接着先拿$q^1$和每个$k$进行match，点乘操作（向量点乘值越大表示向量间的夹角越小，也就表示向量越接近），接着除以$\sqrt d$得到对应的$\alpha$，其中$d$代表向量$k^i$的长度，在本示例中等于2，除以$\sqrt d$的原因在论文中的解释是“进行点乘后的数值很大，导致通过softmax后梯度变的很小”，所以通过除以$\sqrt d$来进行缩放。比如计算$\alpha_{1,i}$：

$$\alpha_{1,1}=\frac{q^1\cdot k^1}{\sqrt d} =\frac{1 \times 1 + 2 \times 0}{\sqrt 2}=0.71$$

$$\alpha_{1,2}=\frac{q^1\cdot k^2}{\sqrt d} =\frac{1 \times 0 + 2 \times 1}{\sqrt 2}=1.41$$

同理拿$q^2$去匹配所有的$k$能得到$\alpha_{2,i}$，统一写成矩阵乘法形式：

$$\left(\begin{matrix} \alpha_{1,1} & \alpha_{1,2} \\ \alpha_{2,1} & \alpha_{2,2}\end{matrix}\right)=\frac{\left(\begin{matrix} q^1\\ q^2\end{matrix}\right) \left(\begin{matrix} k^1\\ k^2\end{matrix}\right)^T}{\sqrt d}$$

接着对每一行即$\left(\begin{matrix} \alpha_{1,1},\alpha_{1,2}\end{matrix}\right)$和$\left(\begin{matrix} \alpha_{2,1},\alpha_{2,2}\end{matrix}\right)$分别进行softmax处理得到$(\hat{\alpha}_{1,1},\hat{\alpha}_{1,2})$和$(\hat{\alpha}_{2,1},\hat{\alpha}_{2,2})$，这里的$\hat{\alpha}$相当于计算得到针对每个$v$的权重。到这我们就完成了$Attention(Q,K,V)$公式中**$softmax(\frac{QK^T}{\sqrt d_k})$**部分。

上面已经计算得到$\alpha$，即针对每个$v$的权重，接着进行加权得到最终结果：

$$b_1=\hat{\alpha}_{1,1} \times v^1 + \hat{\alpha}_{1,2}\times v^2=(0.33,0.67)$$

$$b_2=\hat{\alpha}_{2,1} \times v^1 + \hat{\alpha}_{2,2}\times v^2=(0.50,0.50)$$

统一写成矩阵乘法形式：$$\left(\begin{matrix} b^1\\ b^2\end{matrix}\right)=\left(\begin{matrix} \hat{\alpha}_{1,1} & \hat{\alpha}_{1,2}\\ \hat{\alpha}_{2,1} & \hat{\alpha}_{2,2}\end{matrix}\right)\left(\begin{matrix} v^1\\ v^2\end{matrix}\right)$$

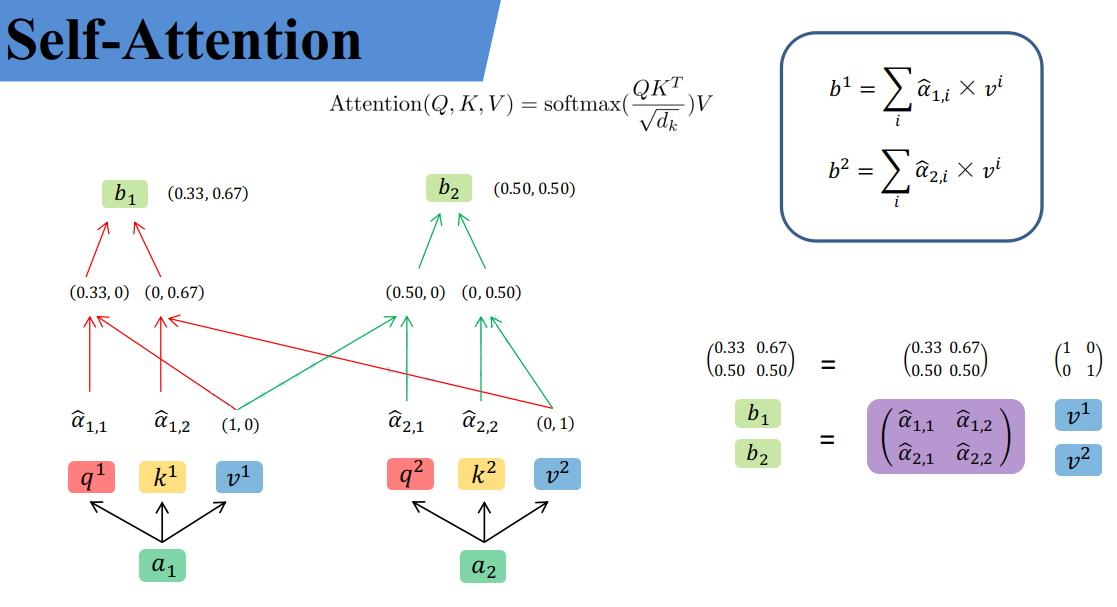
到这，Self-Attention的内容就讲完了。总结下来就是论文中的一个公式：$$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt d_k})V$$

Multi-Head Attention

实际使用中基本使用的还是Multi-Head Attention模块。原论文中说使用多头注意力机制能够联合来自不同head部分学习到的信息。Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions。其实只要懂了Self-Attention模块Multi-Head Attention模块就非常简单了。

首先还是和Self-Attention模块一样将$a_i$分别通过$W_q$，$W_k$，$W_v$得到对应的$q^i$，$k^i$，$v^i$，然后再根据使用的head的数目$h$进一步把得到的$q^i$，$k^i$，$v^i$均分成$h$份。比如下图中假设$h=2$然后$q^1$拆分成$q^{1,1}$和$q^{1,2}$，那么$q^{1,1}$就属于head1，$q^{1,2}$就属于head2。

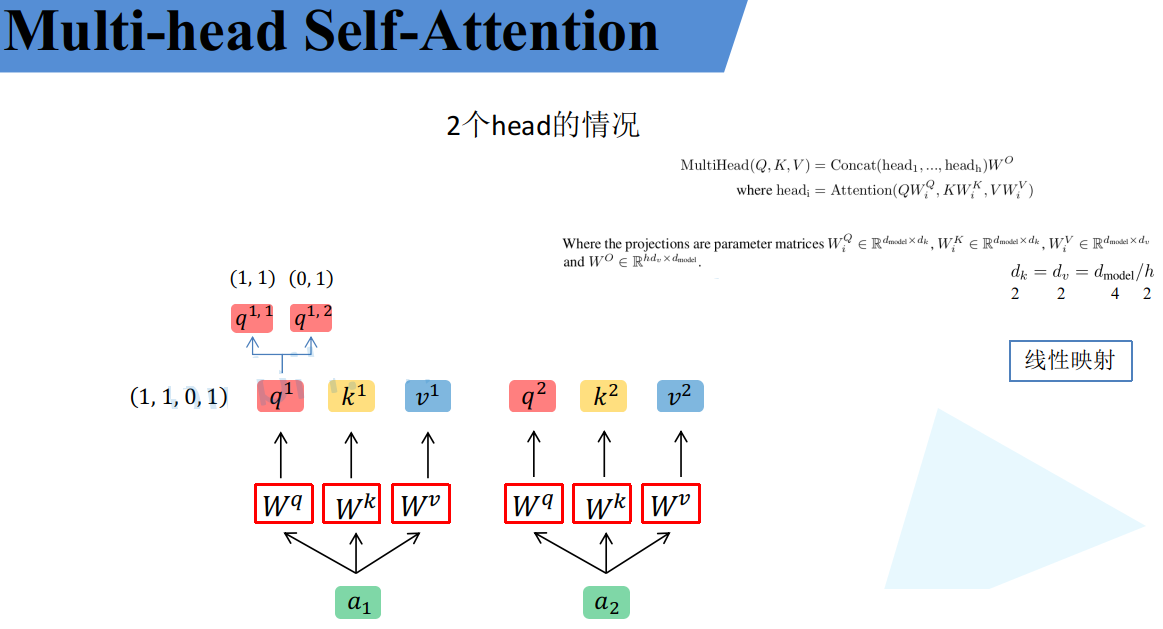
论文中是写的通过$W_i^Q$，$W_i^K$，$W_i^V$映射得到每个head的$Q_i$，$K_i$，$V_i$：$head_i=Attention(QW_i^Q,KW_i^K,VW_i^V)$。但在github上看的一些源码中就是简单的进行均分，其实也可以将$W_i^Q$，$W_i^K$，$W_i^V$设置成对应值来实现均分，比如下图中的$Q$通过$W_1^Q$就能得到均分后的$Q_1$。

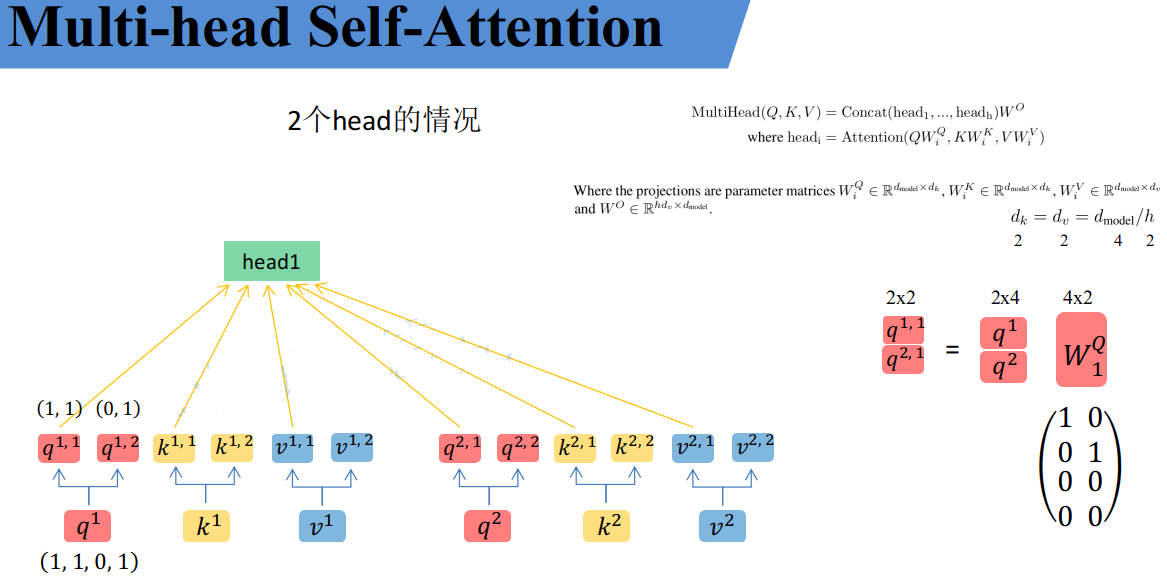
通过上述方法就能得到每个$head_i$对应的$Q^i$，$K^i$，$V^i$参数，接下来针对每个head使用和Self-Attention中相同的方法即可得到对应的结果。$$Attention(Q_i,K_i,V_i)=softmax(\frac{Q_iK_i^T}{\sqrt d_k})V_i$$

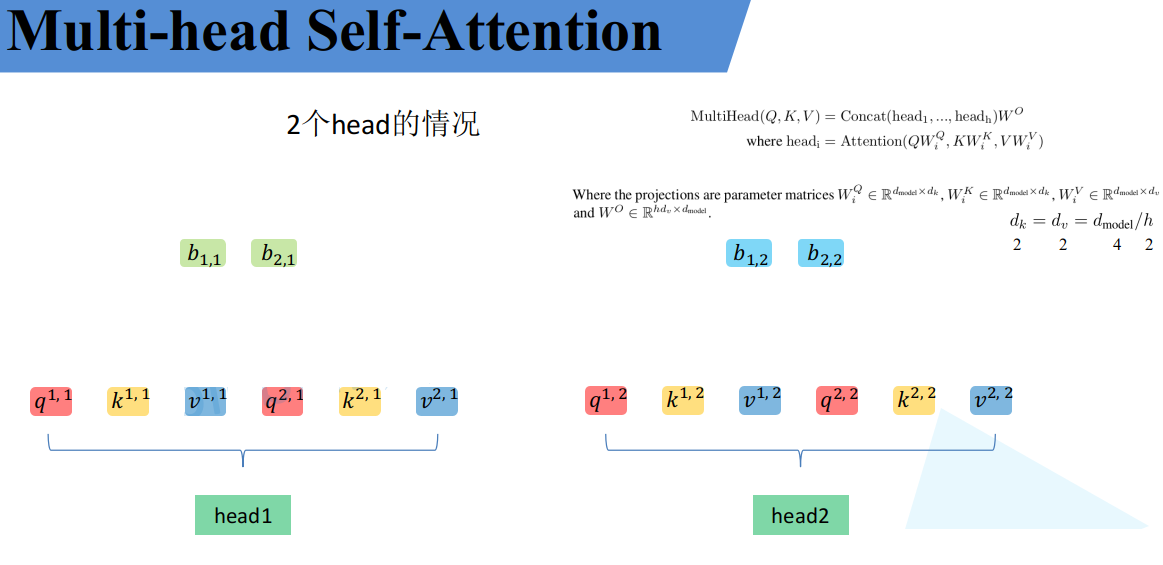
接着将每个head得到的结果进行concat拼接，比如下图中$b_{1,1}$（$head_1$得到的$b_1$）和$b_{1,2}$（$head_2$得到的$b_1$）拼接在一起，$b_{2,1}$（$head_1$得到的$b_2$）和$b_{2,2}$（$head_2$得到的$b_2$）拼接在一起。

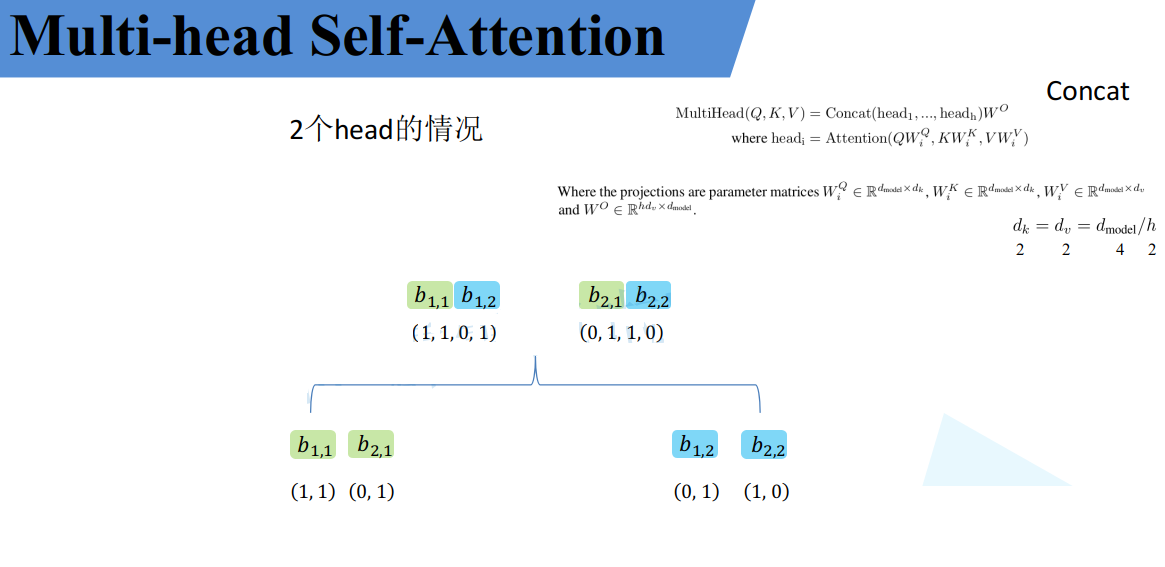
接着将拼接后的结果通过$W^O$（可学习的参数）进行融合，如下图所示，融合后得到最终的结果$b_1$，$b_2$。

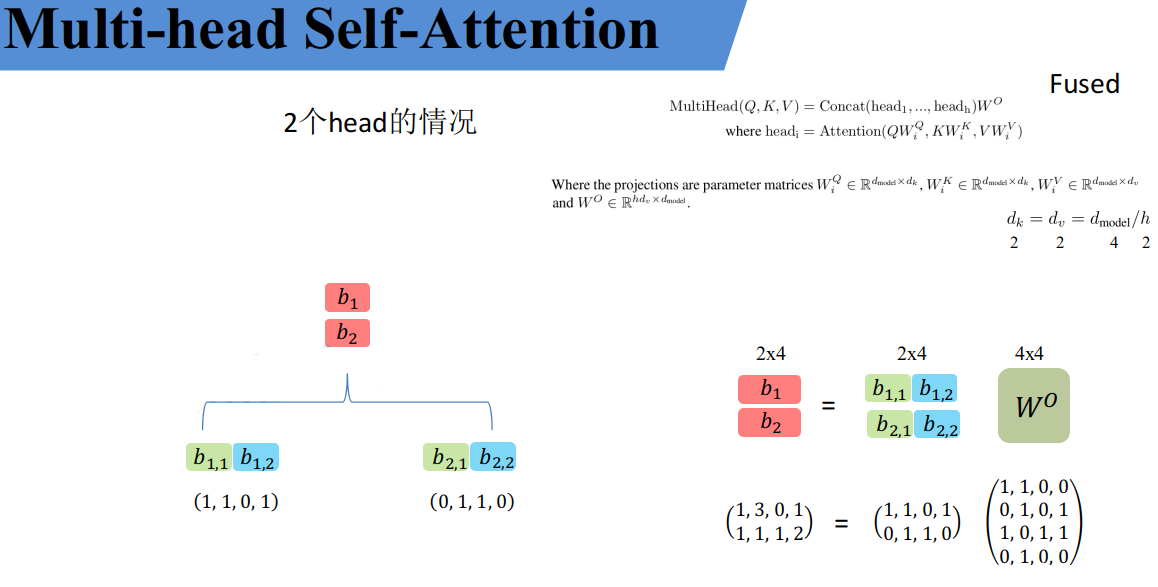
到这，Multi-Head Attention的内容就讲完了。总结下来就是论文中的两个公式：

$$MultHead(Q,K,V)=Concat(head_1,…,head_h)W^O $$

$$ where \space head_i =Attenttion(QW_i^Q,KW_i^K,VW_i^V)$$

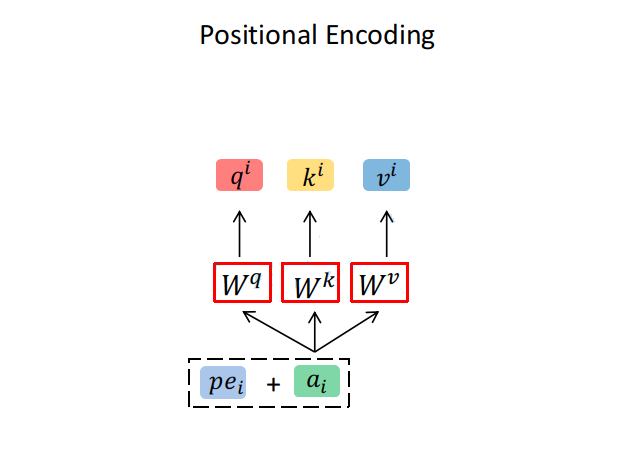
Positional Encoding

刚刚讲的Self-Attention和Multi-Head Attention模块，在计算中是没有考虑到位置信息的。假设在Self-Attention模块中，输入$a_1$，$a_2$，$a_3$得到$b_1$，$b_2$，$b_3$。对于$a_1$而言$a_2$和$a_3$ 离它都是一样近的而且没有先后顺序。假设将输入的顺序改为$a_1$，$a_3$，$a_2$ ，对结果$b_1$是没有任何影响的。（相当于说“我爱你”和“你爱我”意思等同，这样是不对的）

为了引入位置信息，在原论文中引入了位置编码positional encodings。To this end, we add "positional encodings" to the input embeddings at the bottoms of the encoder and decoder stacks.如下图所示，位置编码是直接加在输入的$a={a_1,…a_n}$中的，即$pe={pe_1,…pe_n}$和$a={a_1,…a_n}$拥有相同的维度大小。关于位置编码在原论文中有提出两种方案，一种是原论文中使用的固定编码，即论文中给出的sine and cosine functions方法，按照该方法可计算出位置编码；另一种是可训练的位置编码，作者说尝试了两种方法发现结果差不多（但在ViT论文中使用的是可训练的位置编码）。