深度学习模型之CNN（十三）MobileNetv1v2v3网络详解

MobileNet详解

在传统的卷积神经网络中，内存需求大、运算量大，导致无法在移动设备以及嵌入式设备上运行。在之前学习的网络结构中，例如VGG16的权重大小有400+M、ResNet的152层模型权重大小能到达600+M。如此大的模型参数是不可能在移动设备以及嵌入式设备上运行的。

MobileNet网络是由由google团队在2017年提出的，专注于移动端或者嵌入式设备中的轻量级CNN网络。相比传统卷积神经网络，在准确率小幅降低的前提下大大减少模型参数与运算量。(相比VGG16准确率减少了0.9%，但模型参数只有VGG的1/32)。

MobileNet v1

MobileNetv1版本原论文：MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications

论文网络中的亮点：

• Depthwise Convolution（简称DW卷积，大大减少运算量和参数数量）
• 增加超参数$\alpha$、$\beta$（人为设定，$\alpha$控制卷积层卷积核的个数、$\beta$控制输入图像大小）

DW卷积

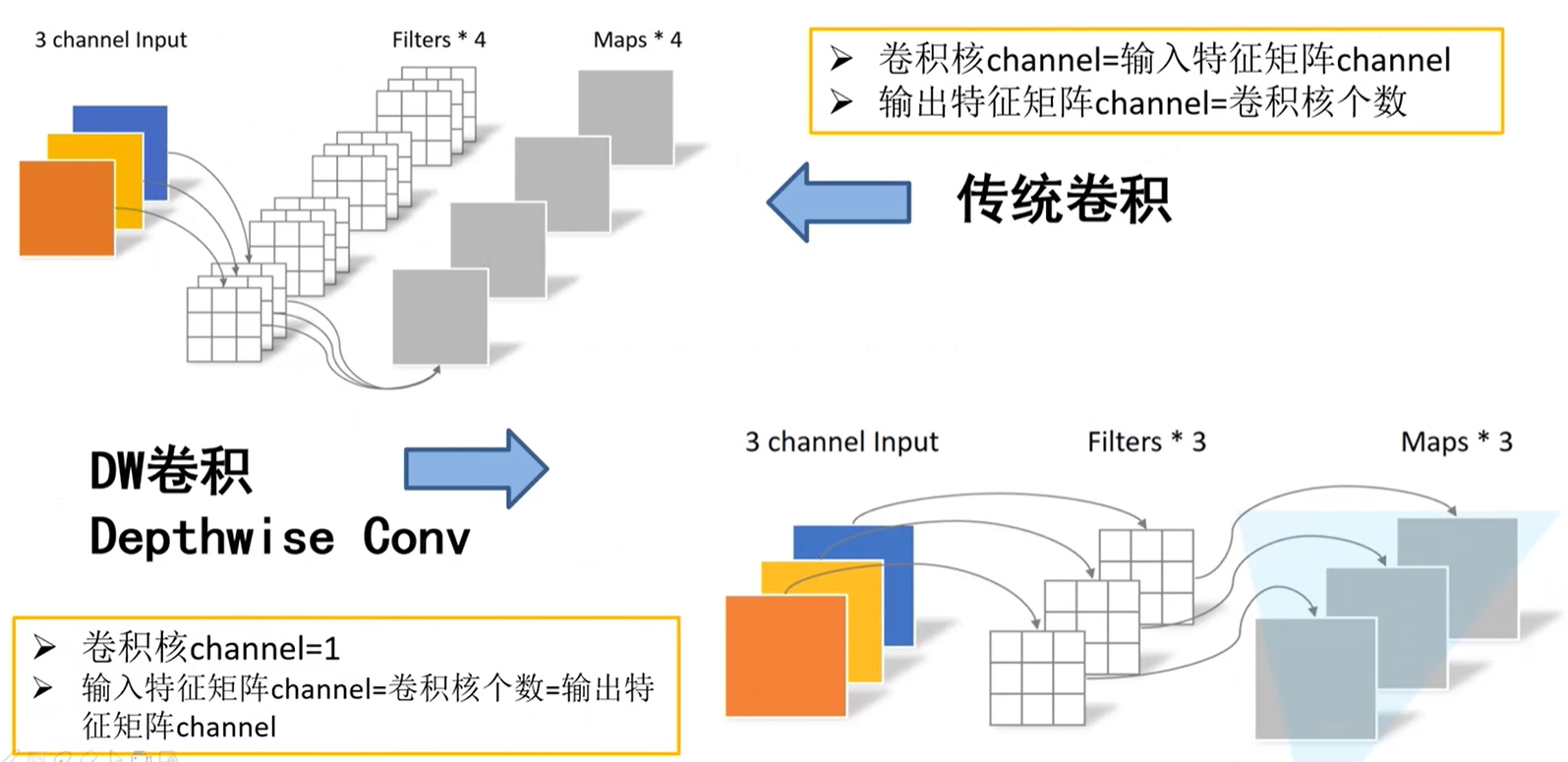
传统卷积过程

输入一个深度为3的特征矩阵，经过4个卷积核进行卷积，每个卷积核的深度与输入特征矩阵的深度是相同的，所以每个卷积核深度也为3。又因输出特征矩阵的深度是由卷积核的个数决定的，因此最终输出特征矩阵的深度为4。

总结：

• 卷积核channel = 输入特征矩阵channel
• 输出特征矩阵channel = 卷积核个数

DW卷积过程

输入一个深度为3的特征矩阵，经过3个卷积核进行卷积，且卷积核深度为1，也就是说一个卷积核对应输入特征矩阵的一个channel，再得到相应的输出特征矩阵的一个channel。既然一个卷积核负责输入特征矩阵的一个深度，那么卷积核的个数应该和输入特征矩阵的深度相同。又因为每一个卷积核与输入特征矩阵的一个channel进行卷积之后得到一个输出特征矩阵的channel，那么输出特征矩阵的深度与卷积核的个数相同，也和输入特征矩阵的深度相同。

总结：

• 卷积核channel = 1
• 输入特征矩阵channel = 卷积核个数 = 输出特征矩阵channel

Depthwise Separable Conv

也叫做深度可分的卷积操作，由两部分组成，第一部分由DW卷积，第二部分为PW卷积。PW卷积实际上相当于普通卷积，只不过卷积核的大小为1。由下图所示，卷积层中卷积核的深度 = 1。

通常情况下DW卷积和PW卷积是一起使用的。

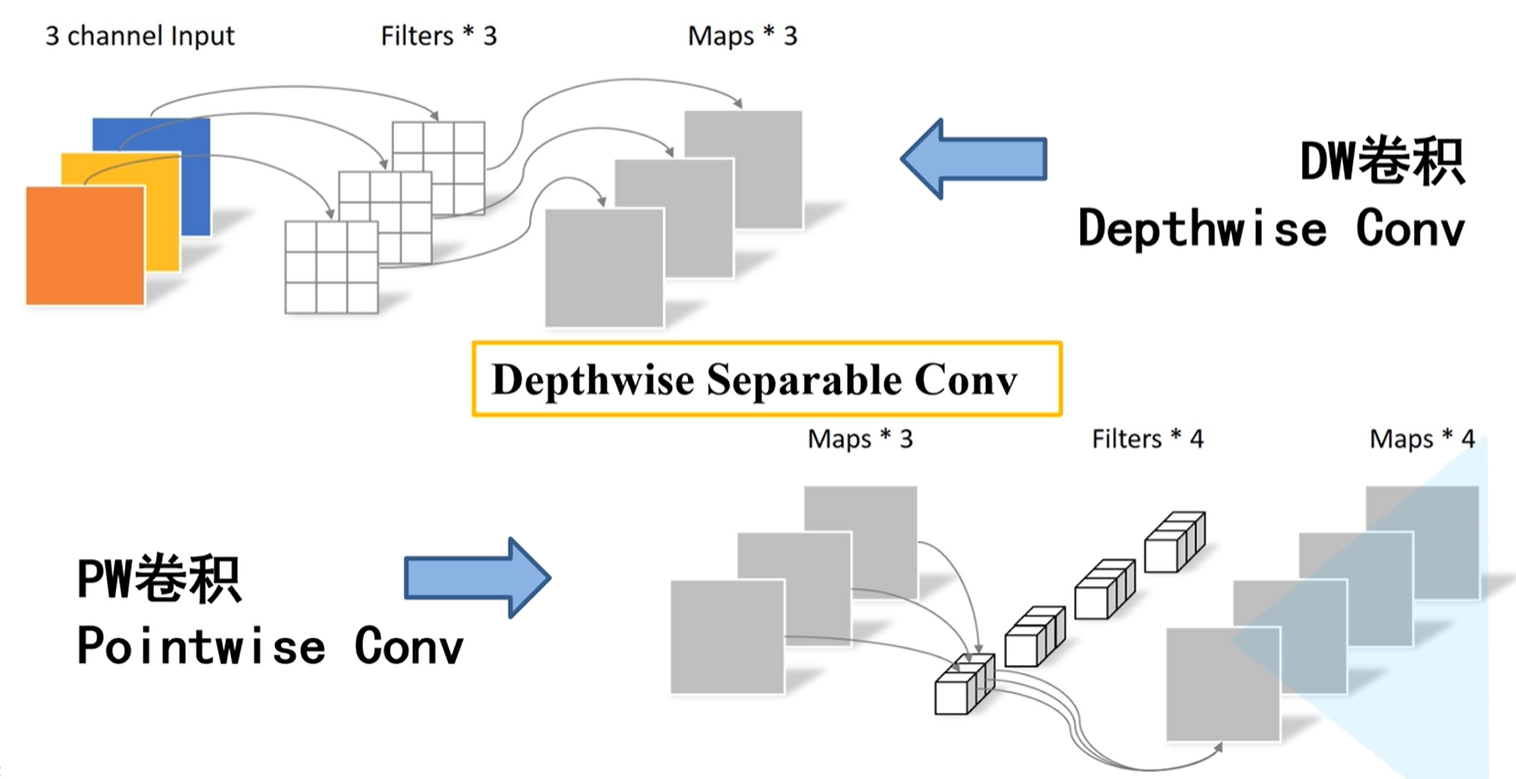
DW&PW卷积和普通卷积的区别

下图（上左）为普通卷积操作，下图（下左）为DW卷积操作，下图（下右）为PW卷积操作，二者结合为深度可分卷积操作。

在普通卷积中，通过卷积操作之后，得到的是channel = 4的特征矩阵；在DW&PW卷积操作之后，得到的同样是channel = 4的特征矩阵。

参数代表含义：$D_F$：输入特征矩阵的宽高；$D_K$：卷积核的大小；M：输入特征矩阵的深度；N：输出特征矩阵的深度

普通卷积计算量：卷积核的高x卷积核的宽x输入特征矩阵的深度x输出特征矩阵的深度x输入特征矩阵的高x输入特征矩阵的宽（默认stride = 1）

DW&PW卷积计算量：

• DW：卷积核的大小x输入特征矩阵的深度x输入特征矩阵的高宽
• PW（相当于普通的卷积）：卷积核的高和宽（都是1）x输入特征矩阵的深度x输出特征矩阵的深度x输入特征矩阵的高宽（默认stride = 1）

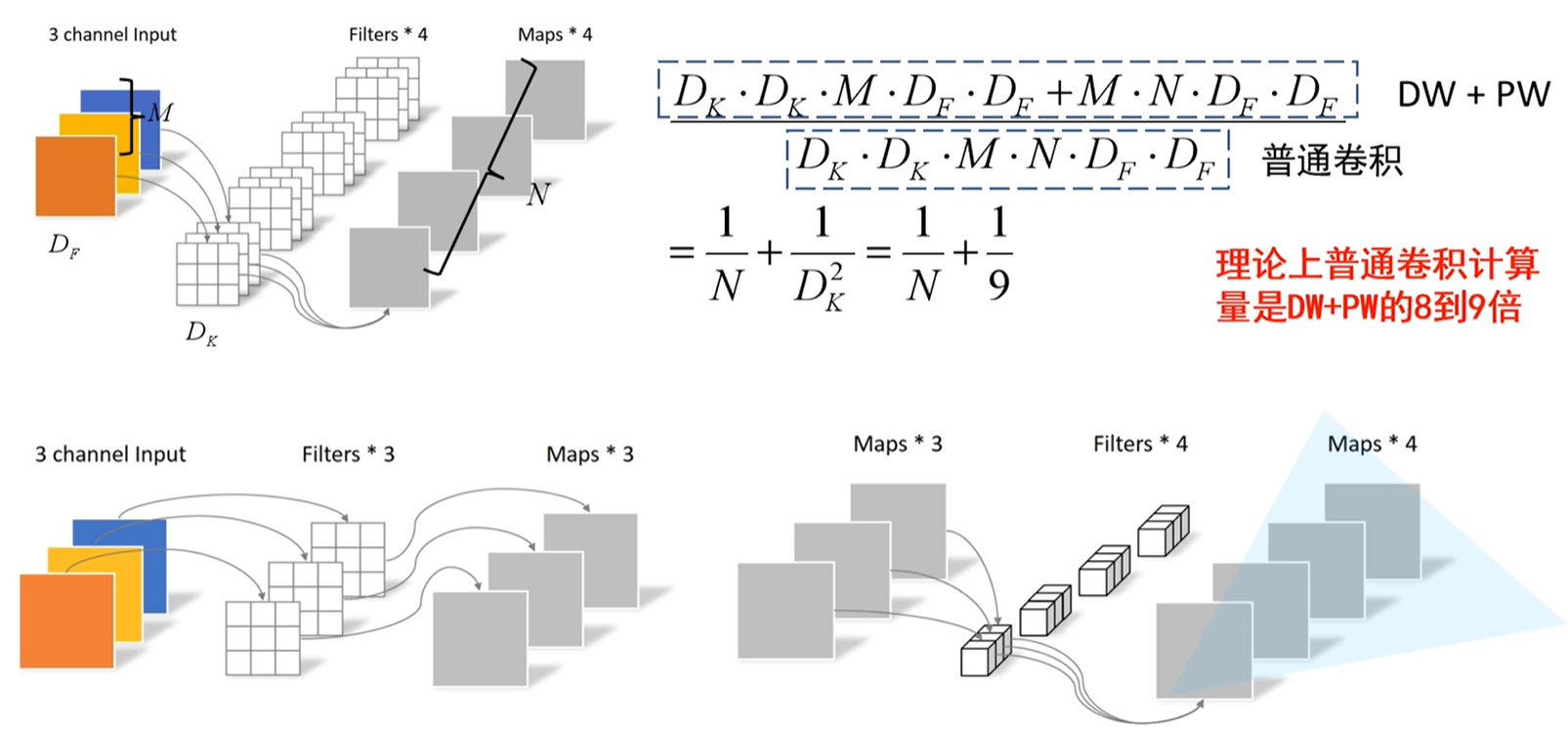
理论上，普通卷积计算量是DW&PW卷积的8~9倍

MobileNet v1网络结构参数

Filter Shape：3 x 3 x 3 x 32分别指的是卷积核的高宽、深度、个数

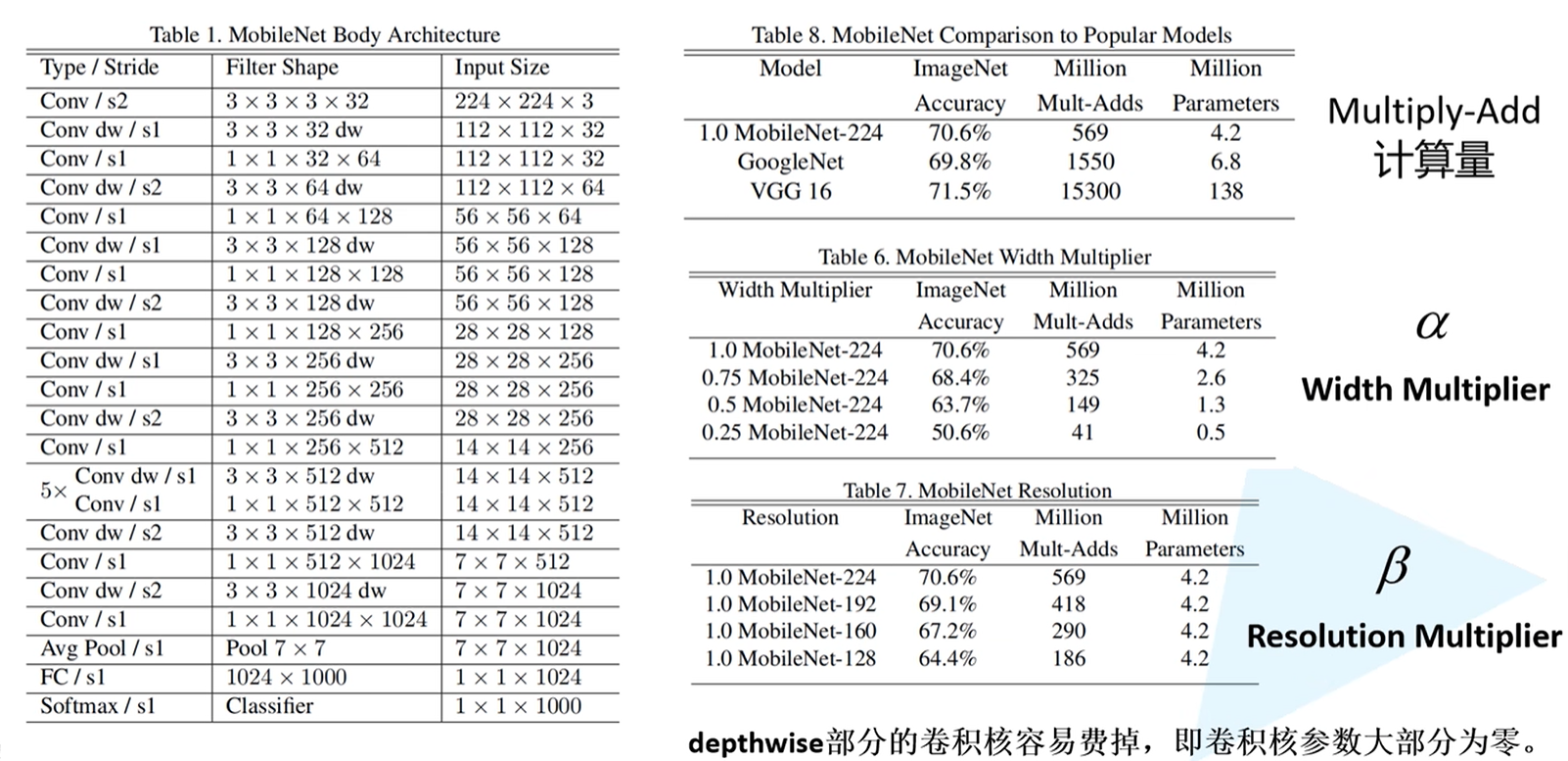
超参数$\alpha$、$\beta$

• $\alpha$：卷积核个数的倍率，用来控制卷积过程中所采用卷积核的个数
• $\beta$：分辨率的参数，用来控制输入图像的大小

大多数人发现，DW卷积在训练完之后的部分卷积核容易废掉，即卷积核参数大部分为0，也就是说DW卷积核没有起到作用。针对这个问题，在MobileNet v2版本中有一定的改善。

MobileNet v2

MobileNet v2网络是由google团队在2018年提出的，相比MobileNet v1网络，准确率更高，模型更小。原论文：MobileNetV2: Inverted Residuals and Linear Bottlenecks

网络中的亮点：

• Inverted Residuals（倒残差结构）
• Linear Bottlenecks

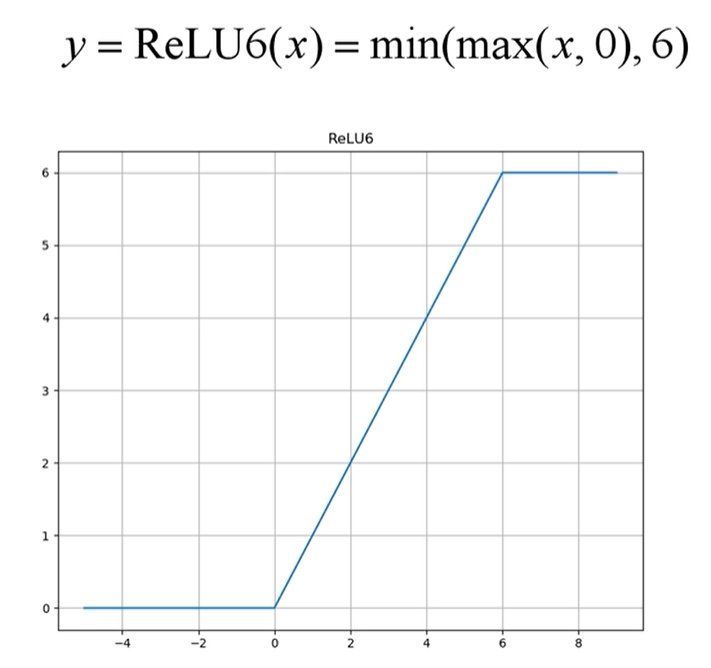
Inverted Residuals

Residual block

对输入特征矩阵采用1x1卷积核进行降维处理，之后经过3x3的卷积核及逆行卷积处理，再通过1x1的卷积核进行升维，之后再输出特征矩阵。这就形成两边大中间小的瓶颈结构。

注意：采用ReLU激活函数

Inverted residual block

对输入特征矩阵采用1x1卷积核进行升维处理，之后经过3x3的卷积核进行DW卷积，再通过1x1的卷积核进行降维处理，之后在输出特征矩阵。这就形成两边小中间大的橄榄球结构。

注意：采用ReLU6激活函数

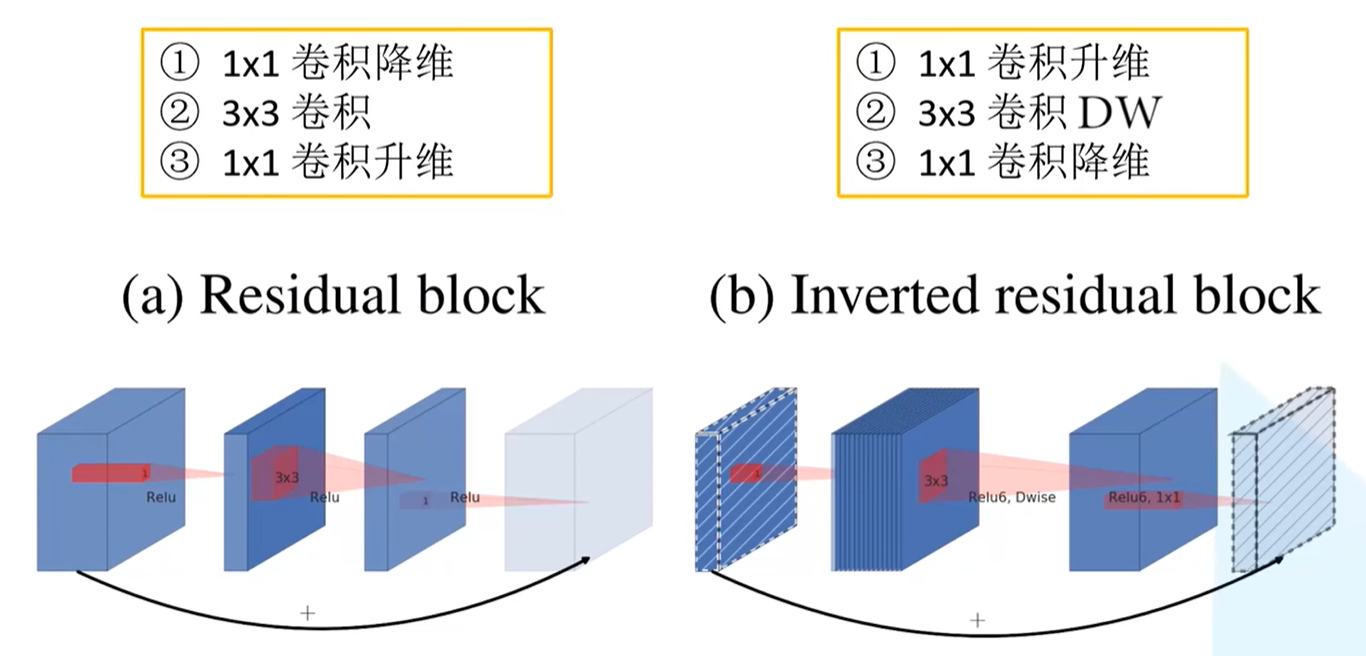
ReLU6激活函数

在普通的ReLU激活函数中，当输入值<0时，默认将输出置0；当输入值>0时，即不进行处理。在ReLU6激活函数中，在输入值<0，以及 [ 0, 6 ] 的区间时处理都一致，但在输入值>6时，将会将输出值一直为6。

Linear Bottlenecks

在论文中是针对Inverted residual结构的最后一个1x1的卷积层，使用线性激活函数而不是之前的ReLU激活函数。在下图中是作者在原文中描述为什么在最后一个1x1卷积层不使用ReLU激活函数原因的实验证明。

首先输入的是一个2维矩阵，channel = 1；之后采用不同维度的matrix T 将输入进行变化，变化到更高的维度，再通过ReLU激活函数得到输出值。之后再使用T矩阵的逆矩阵$T^{-1}$，将输出的矩阵还原回2维的矩阵。当matrix T的维度是2，3的时候（即还原回去之后），所对应的即是图中的Output/dim = 2，Output/dim = 3

由图中可以看到，当被还原之后，图像中已经丢失了很多信息，随着matrix T维度不断的加深，丢失的信息就越来越少。因此ReLU激活函数对低维特征信息造成大量损失，而对于高维特征信息造成的损失很小

而在Inverted residual结构当中，是两边细、中间粗的结构，因此在输出时是一个低维的特征向量，需要一个线性的激活函数来替代ReLU激活函数，来避免特征信息的损失。

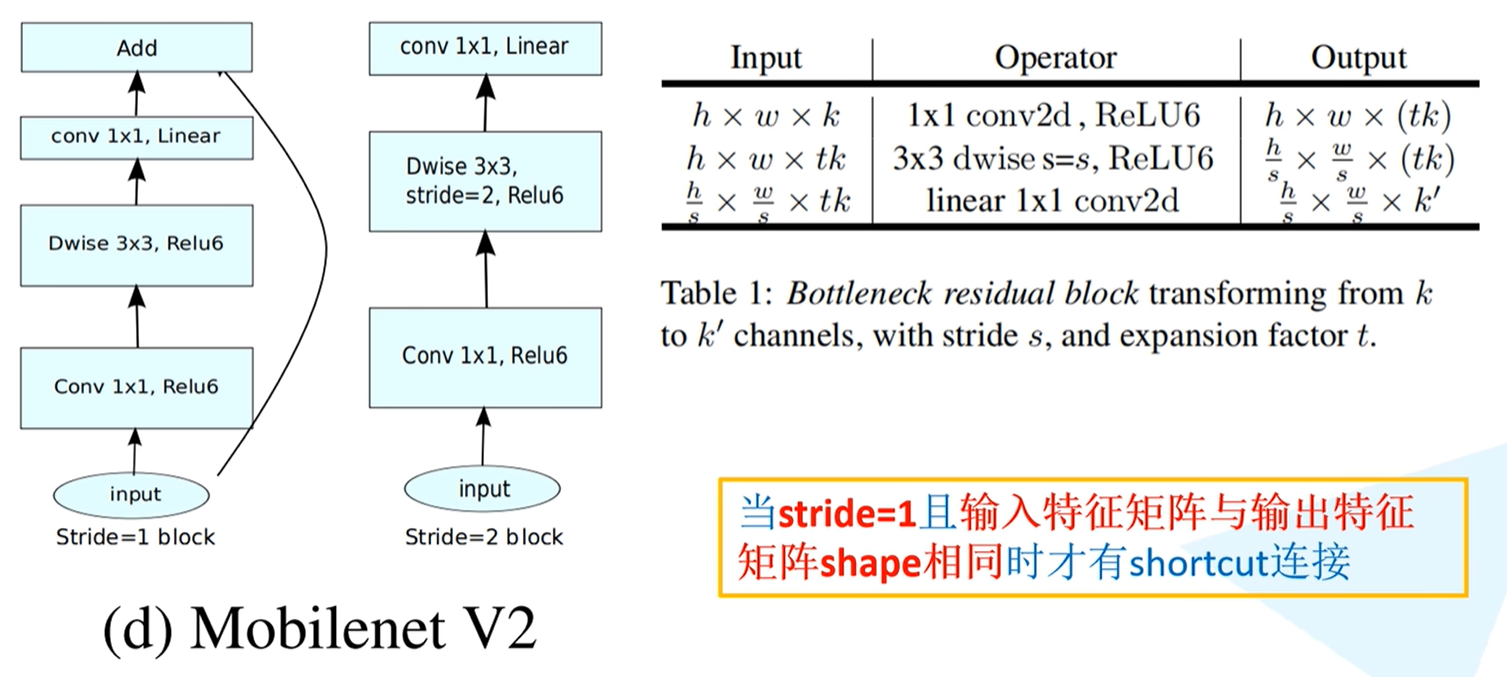
Inverted residual网络结构图

Inverted residual网络结构如下图（左），首先通过1x1的卷积层进行卷积，通过ReLU6激活函数进行激活，之后通过DW卷积，卷积核大小为3x3，同样通过ReLU6激活函数激活，最后经过卷积核大小为1x1的卷积处理，使用线性激活函数。

过程信息为下图（右）表格，首先通过1x1卷积层进行升维处理（输出深度为tk，也就是说这里采用的卷积核的个数是tk个）；在第二层中，输入特征矩阵的深度为上一层的输出，即tk，这里采用卷积核大小为3x3的DW卷积，stride = s，由前文可知此处深度不变，依旧是tk，但高宽缩减s倍；最后一层通过1x1卷积核进行降维处理，卷积核个数为k‘。

注意：**在MobileNet v2版本中，并不是每一个Inverted residual结构中都有shortcut。**在论文中，表述当stride = 1时，是有shortcut，当stride = 2时，是没有shortcut。但通过搭建网络结构之后，会发现论文此处表述有误，正确表述应该为：当stride = 1且输入特征矩阵与输出特征矩阵shape相同时才有shortcut连接。

MobileNet v2网络结构参数

相关参数介绍：

• t：扩展因子，对应着第一层1x1的卷积层所采用的卷积核个数的拓展倍率
• c：时输出特征矩阵的深度channel，即是上图中提到的k’，控制着输出特征矩阵的深度
• n：bottleneck的重复次数，此处的bottleneck指的是论文中的Inverted residual结构
• s：步距，仅仅针对每一个block所对应的第一层bottleneck的步距（一个block由一系列bottleneck组成），其他都为1。假设当n = 2时，即bottleneck需要重复2遍，对于这个结构而言，第一层的步距是2，第二层s为1。

注意：在第一个bottleneck中，t = 1，即该处的扩展因子为1，也就是说在第一层卷积层是没有对特征矩阵的深度做调整的。因此在搭建网络时，因为这一层卷积层没有起到升维或者降维作用，所以会被跳过，直接进入3x3的卷积层中处理。

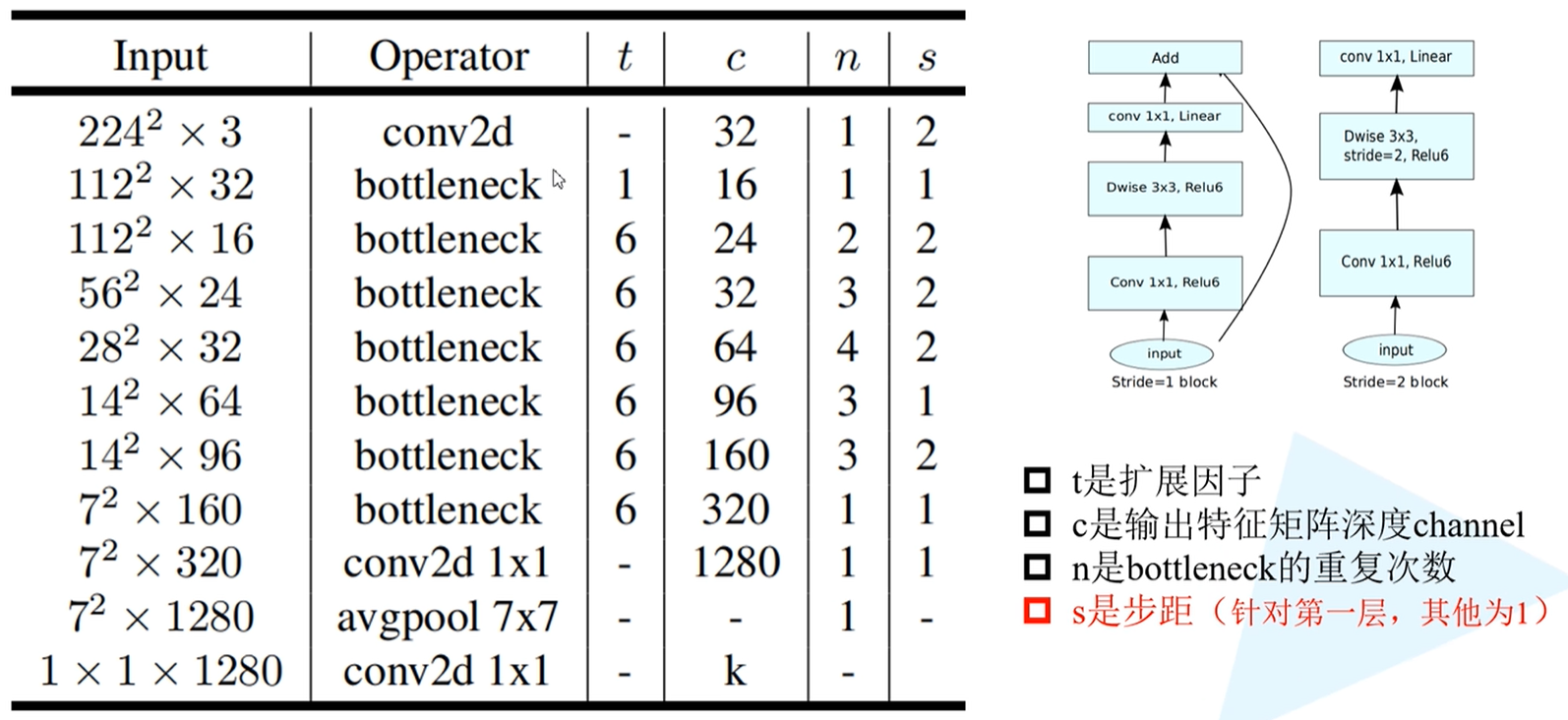
如何理解有无shortcut？

以输入为$14^2$x64这一行的block来举例，这一行的block采用了3个bottleneck结构，stride = 1，即此处block的第一层卷积层的stride = 1，如果按照官方标注而言，应该需要由shortcut。

但实际上这里不可能有shortcut，因此此处的输入特征矩阵的深度为64，但是输出特征矩阵的深度是96。也就是说，如果有shortcut的话，那么输出特征矩阵的深度应该是64，但从表中可知经过一系列操作后输出的特征矩阵深度是96，所以两个特征矩阵的深度是不相同的，无法相加。

在第二层的时候，s = 1，这里的输入特征矩阵深度是上一层的输出特征矩阵深度，即96，对于第二层bottleneck而言，输入的特征矩阵深度十96，其输出特征矩阵的深度也是96，有因为stride = 1，特征矩阵的高宽不会发生变化，因此满足输入特征矩阵和输出特征矩阵的shape保持一致的条件，此时才能使用shortcut。

因此，只有当stride = 1且输入特征矩阵与输出特征矩阵shape相同时才有shortcut连接。

conv2d 1x1

网络结构最后一层是卷积层，输入特征矩阵为1x1x1280，实际上这一层就是一个全连接层，功能上二者一模一样。k表示的是分类的类别个数，若针对ImageNet而言，这里的k = 1000。

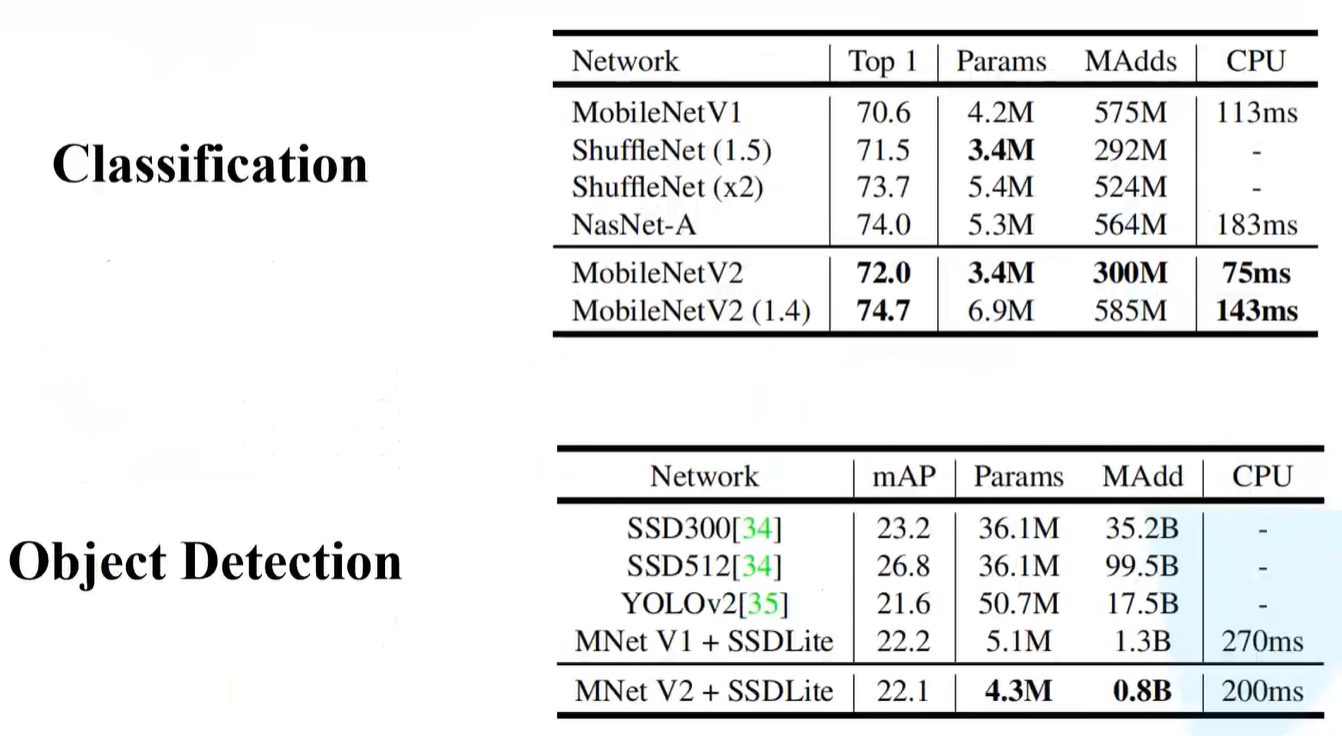
性能对比

表头对应为：准确率、模型参数、运算量、运算时间。

• 下图（上）是针对在分类任务中的性能对比，MobileNetV2（1.4）指的是$\alpha$ = 1.4（倍率因子）；
• 下图（下）是针对在目标检测中的效果对比，将MNet V2与SSDLite联合使用，将MNet v2作为前置网络，SSDLite将其中的一些卷积层换为深度可分卷积，也就是DW卷积+PW卷积。

MobileNet v3

原论文：Searching for MobileNetV3

论文中的亮点：

• 更新Block（bneck）（即对Inverted residual结构基础上，进行简单改动）
• 使用NAS搜索参数（Neural Architecture Search）
• 重新设计耗时层结构（NAS搜索之后得到的网络，之后对网络的每一层的推理时间进行分析，针对某些耗时的层结构做进一步的优化）

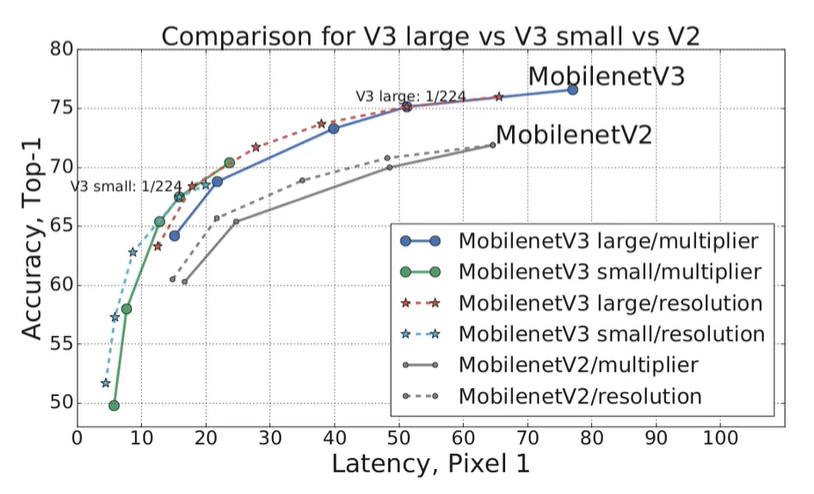
性能对比

在原论文的摘要中，作者提到，v3版本的Large对比v2而言在图像分类任务当中准确率上升有3.2%，延迟有降低20%。

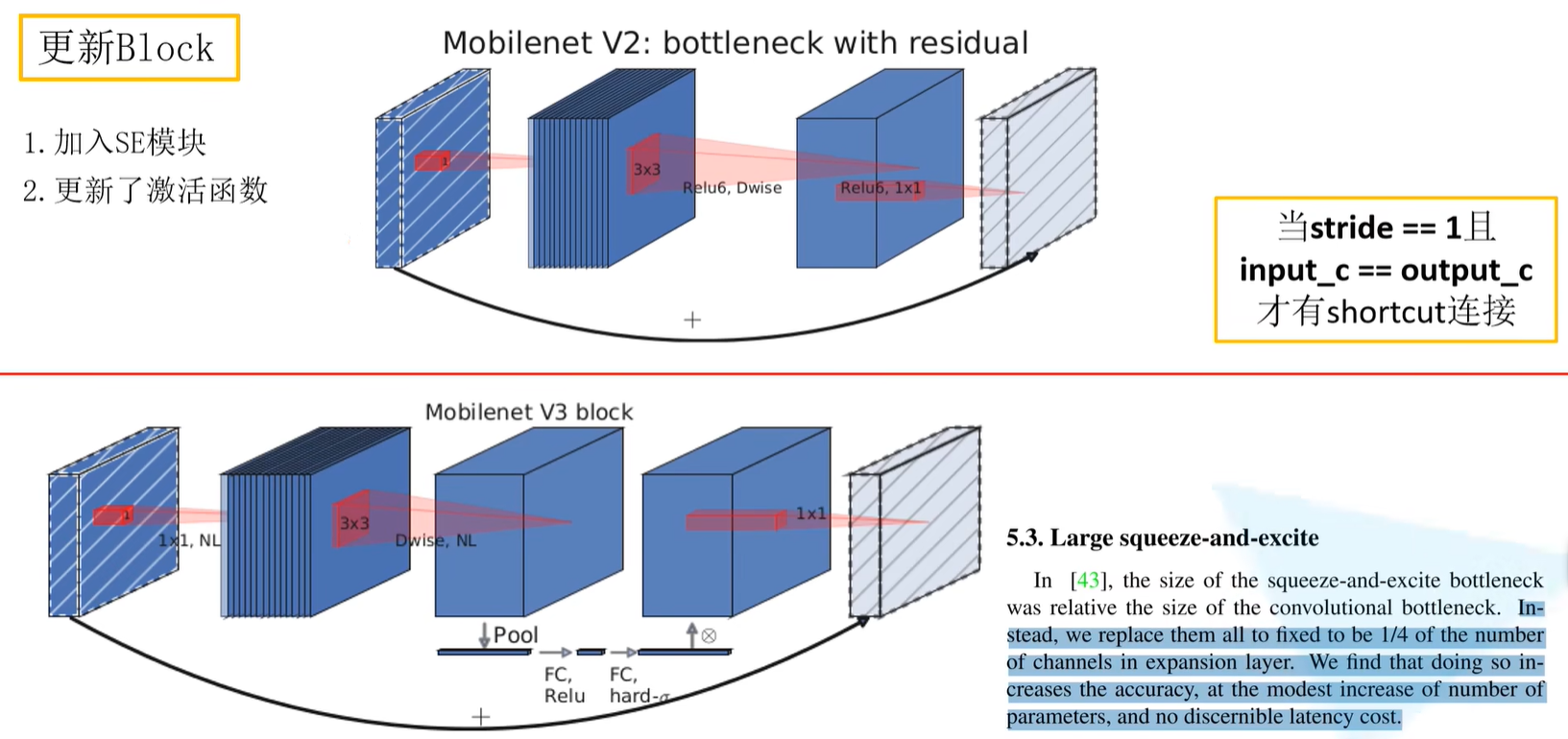
更新Block

在v3当中，做出了Block的更新：

• 加入SE模块，即通道的注意力机制模块
• 更新了激活函数

Mobilenet V2：bottleneck with residual

在v2当中，会首先通过1x1的卷积核对输入特征矩阵进行升维处理，之后通过BN，ReLU6激活函数，之后是通过3x3的DW卷积，之后进行BN，ReLU激活函数激活，最后通过1x1卷积层进行降维处理，之后只跟了一个BN结构，并没有像前面几层一样还有一个ReLU6激活函数。最后有一个shortcut相加处理。

注意：当stride = 1且input_c = output_c才有shortcut连接

Mobilenet V3 block

加入SE模块

大部分框架与v2保持一致，但是在第二层卷积层中加入了SE注意力机制。也就是说针对得到的特征矩阵，对每个channel进行池化处理，那么特征矩阵的channel是多少，得到的1维向量就有多少元素，之后再通过两个全连接层得到输出向量。

注意：

• 对于第一个全连接层，此处的节点个数 = 该处卷积层特征矩阵channel的1/4（在v3原论文中作者有给出）
• 第二层全连接层的节点个数 = 该处卷积层特征矩阵channel
• 对于输出的向量，可以理解为是对该层卷积层特征矩阵的每一个channel分析出了一个权重关系，觉得比较重要的channel会赋予更大的权重，觉得不是那么重要的channel的维度上就对应较小的权重。

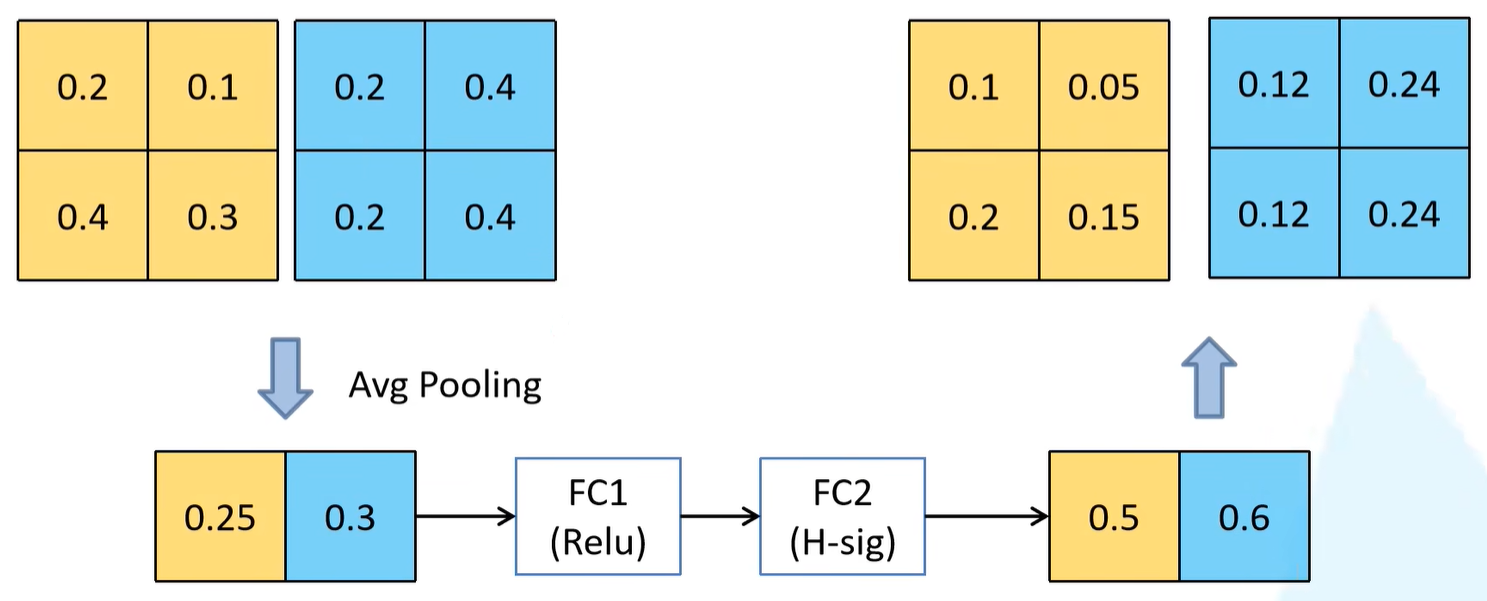
理解两处的全连接层

假设此处特征矩阵的channel = 2，首先通过平均池化下采样层操作对每一个channel取一个均值，由于有两个channel，所以得到一个元素个数为2的向量。之后再依次通过两个全连接层，得到输出。

针对FC1，节点个数= 输入特征矩阵channel的1/4，实际情况中channel会很多，不会出现小于4的情况。之后跟着一个ReLU激活函数。对于FC2而言，节点个数 = 输入特征矩阵channel = 2，之后跟着H-sig激活函数（之后讲解）。

之后会得到有2个元素的向量，每一个元素对应的就是每一个channel所对应的权重。比如预测第一个channel的权重 = 0.5，那么就将0.5与第一个channel的当中的所有元素相乘得到一个新的channel数据。

更新激活函数

在v3的Block中所使用的激活函数标注的都是NL激活函数，即非线性激活函数的意思。因为在不同的层之间所使用的激活函数都不一样，因此在下图中并未给出明确的激活函数名称。

注意：在最后一个标注的1x1降维的卷积层中，是没有使用激活函数的，也可以说使用了一个线性激活函数y = x。

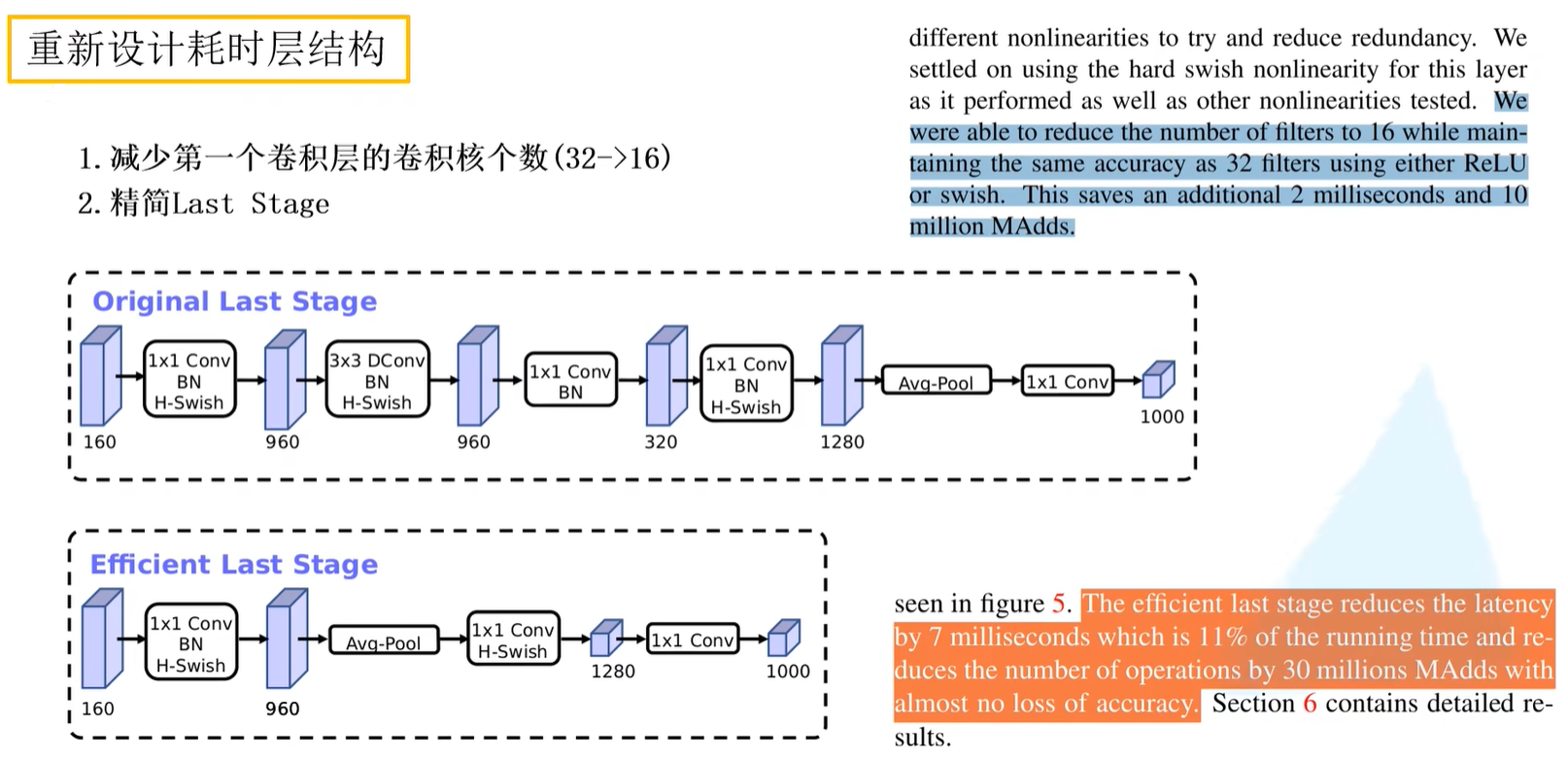
重新设计耗时层结构

• 减少第一个卷积层的卷积核个数（32->16）

  ​ 在原论文当中，作者提到当卷积核个数变化了之后，准确率是没有变化的，那么就达成了在维持准确率不降的前提下减少计算量的目的，这里大概减少2ms的时间

• 精简Last Stage

  ​ 在通过NAS搜索出来的网络结构的最后一个部分叫做Original Last Stage，作者在原论文中发现，这一个流程是比较耗时的，因此作者针对这个结构做出精简化，于是提出了Efficient Last Stage。

  ​ 在精简之后发现，第一个卷积层是没有发生变化的，紧接着直接进行平均池化操作，然后跟着两个卷积核输出。和下图（上）的结构对比而言，减少了许多层结构。调整之后，作者发现准确率无多少变化，但执行时间上减少了7ms，这7ms占据整个推理时间的11%。

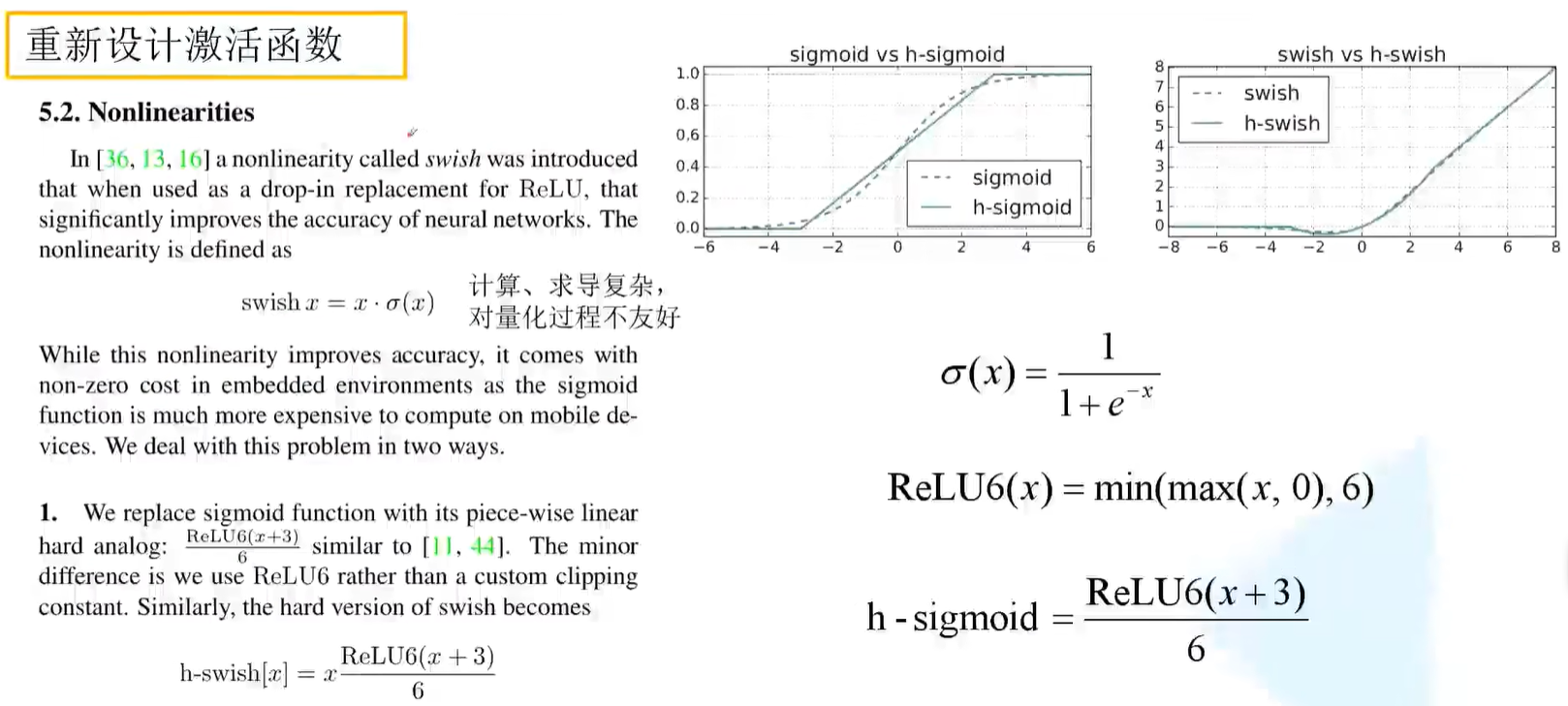
重新设计激活函数

在v2网络结构中，基本使用的激活函数都是ReLU6，目前来说比较常用的激活函数叫做swish激活函数，也就是输入值*sigmoid函数。使用swish激活函数确实会提高网络的准确率，但是在计算、求导上非常复杂，对量化过程也不友好（将模型部署到硬件设备上）。

于是作者提出h-swish激活函数，也就是输入值*h-sigmoid函数，其中h-sigmoid = ReLU6（x+3）/6，也就是在ReLU函数的输入值基础上+3的值除以6。

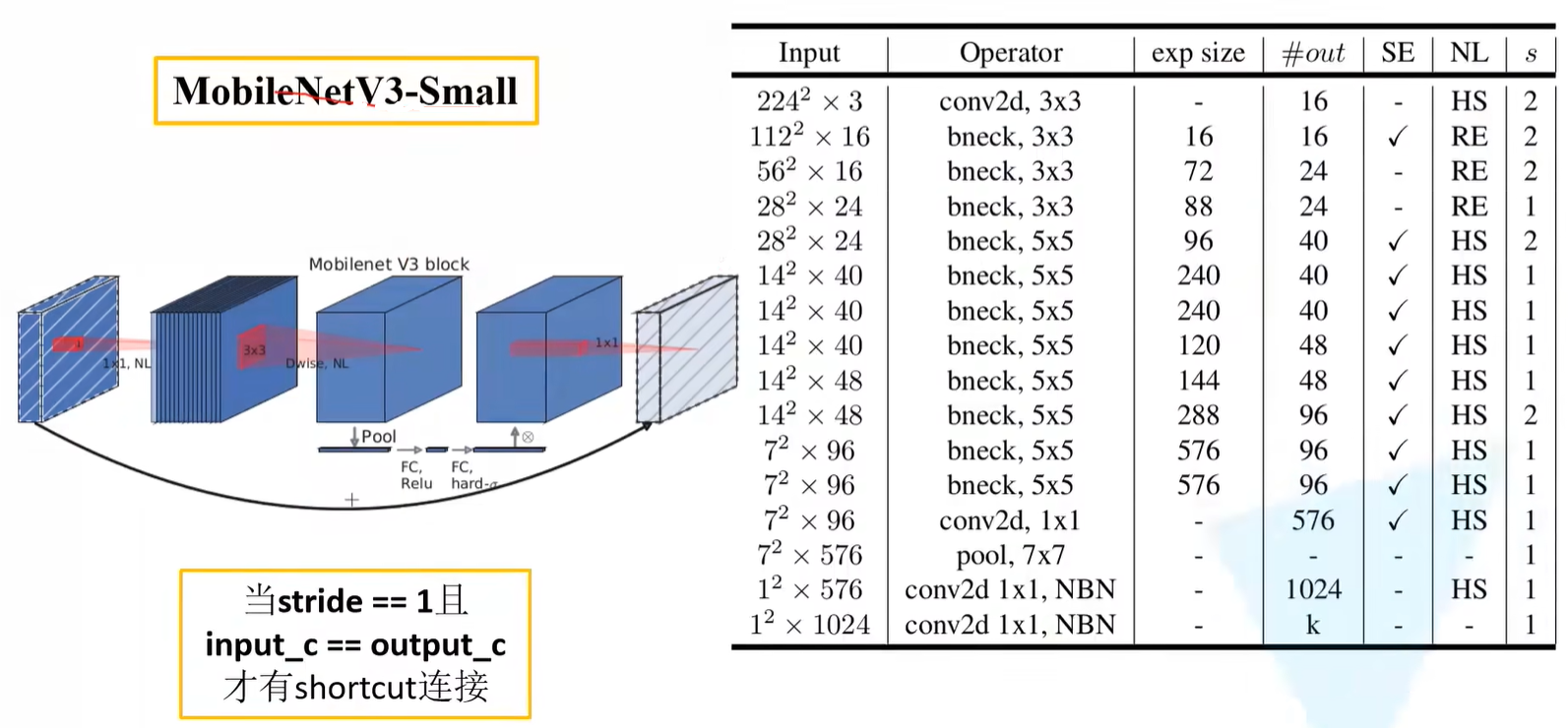
V3-Large网络结构参数

• input：输入特征矩阵的长宽深；
• Operator：对应操作，例如第一层进行conv2d操作；bneck指进行的block操作，其中3x3指的是下图（左）中的DW卷积中卷积核的大小
• exp size：代表第一个升维的1x1卷积需要将维度升到多少
• #out：输出特征矩阵的channel；
• SE：是否使用注意力机制
• NL：使用的激活函数，HS指H-swish激活函数，RE指ReLU6激活函数
• s：表示DW卷积中的步距stride

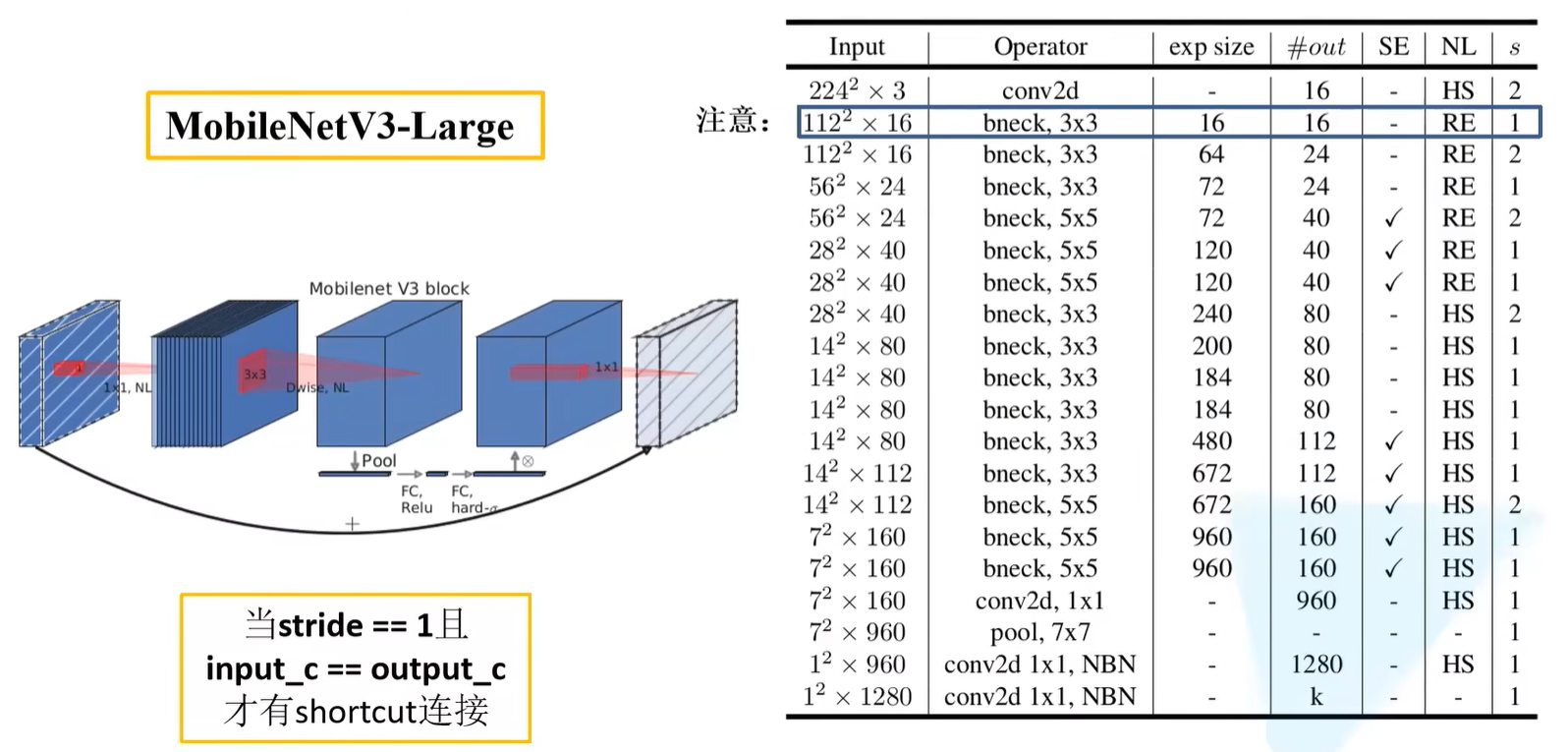
最后两层有写到NBN结构，指的是不去使用，和全连接层的作用是差不多的，这里直接使用卷积结构。

注意：在第一个bneck结构的第一层卷积层之中，因为i输入的特征矩阵channel = 16且输出的特征矩阵channel = 16，因此没有进行升维和降维，且没有SE结构，直接进行1x1的卷积层输出就没有了，因此在搭建网络中，会省略这一步。

V3-Small网络结构参数