数据结构之图

发表于 更新于 分类于 阅读次数： Valine： 本文字数： 5.9k 阅读时长 ≈ 5 分钟

第八章图

第一节图的概念和存储结构

1.概念

线性表可以为空，树可以为空，但是图不能为空。图中不能一个顶点也没有，图的顶点集V一定非空，但边集E可以为空，此时图中只有顶点而没有边。

（1）有向图
$$
G_1 = (V_1,E_1)\
V_1 = {1,2,3}\
$$

$$
E_1 = {<1,2>,<2,1>,<2,3>}
$$

graph LR;
A((1))
B((2))
C((3))
A-->B
B-->A
B-->C

（2）无向图
$$
G_1 = (V_1,E_1)\
V_1 = {1,2,3,4}\
$$

$$
E_1 = {(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}
$$

（3）简单图、多重图

  • 简单图：①不存在重复边；②不存在顶点到自身的边。
  • 多重图：图G中某两个顶点之间的边数大于1条，有允许顶点通过一条边和自身关联。

（4）完全图（简单完全图）
$$
\begin{flalign}
&无向完全图|E|取值范围 = [0,n(n-1)/2]\
&有向完全图|E|取值范围 = [0,n(n-1)~~~~]
\end{flalign}
$$
（5）子图：G = (V，E)和G = (V，E)，若V是V的子集，且E`是E的子集

（6）连通、连通图和连通分量（无向图）

  • 连通：无向图，顶点v和顶点w有路径存在，则称v和w是连通的
  • 连通图：无向图图G任意两个顶点都是连通的，称连通图，否则为非连通图
  • 连通分量：无向图的极大连通子图

（7）强连通图、强连通分量（有向图）

  • 强连通：有向图，有一对顶点v和w，从v到w和w到v之间都有路径，则称两个顶点是强连通的
  • 强连通图：任意一对顶点都是强连通的
  • 强连通分量：有向图中的极大强连通分量

（8）生成树、生成森林

连通图的生成树是包含图中全部顶点的一个极小连通子图。若顶点数为n，则生成树含有n-1条边

（9）顶点的度、入度和出度
$$
\begin{flalign}
&n个顶点e条边的无向图:\sum_{i=1}^nTD(v_i) = 2e\
&n个顶点e条边的有向图：\sum_{i=1}^nID(v_i) = \sum_{i=1}^nOD(v_i) = e
\end{flalign}
$$
（10）路径、路径长度、回路

若有一个图有n个顶点，并且有大于n-1条边，则该图一定有环

（11）简单路径、简单贿赂

  • 简单路径：顶点不重复出现的路径
  • 简单回路：除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路

2.存储结构

（1）邻接矩阵法

空间复杂度O(n^2)

无权图
$$
A[i][j] =
\begin{cases}
1,~~~~~~~若(v_i,v_j)或<v_i.v_j>是E(G)中的边\\
0,~~~~~~~若(v_i,v_j)或<v_i.v_j>不是E(G)中的边\
\end{cases}
$$
​ 举例如下：

graph LR;
A((1))
B((2))
C((3))
D((4))
A-->B
A-->C
C-->D
D-->A

$$
A_1=\left[
\matrix{
0 & 1 & 1 & 0\
0 & 0 & 0 & 0\
0 & 0 & 0 & 1\
1 & 0 & 0 & 0\
}
\right]
$$

有权图
$$
A[i][j] =
\begin{cases}
w_{ij},~~~~~~~~~~~若(v_i,v_j)或<v_i.v_j>是E(G)中的边\\
0或∞,~~~~~~~若(v_i,v_j)或<v_i.v_j>不是E(G)中的边\
\end{cases}
$$
举例如下：

graph LR;
A((1))
B((2))
C((3))
D((4))
A--5-->B
A--8-->C
C--10-->D
D--21-->A

$$
A_2=\left[
\matrix{
∞ & 5 & 8 & ∞\
∞ & ∞ & ∞ & ∞\
∞ & ∞ & ∞ & 10\
21 & ∞ & ∞ & ∞\
}
\right]
$$

存储结构定义：

1
2
3
4
5
6
7
8
#define MaxVertextNum 100							//顶点数目的最大值
typedef char VertexType;							//顶点的数据类型
typedef int EdgeType;								//带权图中边上权值的数据类型
typedef struct{
    VertexType Vex[MaxVertextNum];						//顶点表
    Edgetype Edge[MaxVertextNum][MaxVertextNum];		//邻接矩阵，边表
    int vexnum,arcnum;									//图的当前顶点数和弧数
}MGraph;

（2）邻接表法

  • 无向图：存储空间O(|V|+2|E|)
  • 有向图：存储空间O(|V|+|E|)

顶点表结点结构

顶点域 边表头指针
data firstarc

边表结点结构

邻接点域 指针域
adjvex nextarc

存储结构定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#define MaxVertexNum 100							//顶点数目的最大值
typedef struct ArcNode{								//边表结点
    int adjvex;									//该弧所指向的顶点的位置
    struct ArcNode *next;						//指向下一条弧的指针
    //InfoType info;							//网的边权值
}ArcNode;
typedef struct VNode{							//顶点表结点
    VertexType data;							//顶点信息
    ArcNode *first;								//指向第一条依附该顶点的弧的指针
}VNode,AdiList[MaxVertexNum];
typedef struct{
    AdiList vertices;							//邻接表
    int vexnum,arcnum;							//图的顶点数和弧数
}ALGraph;										//ALGraph是以邻接表存储的图的类型

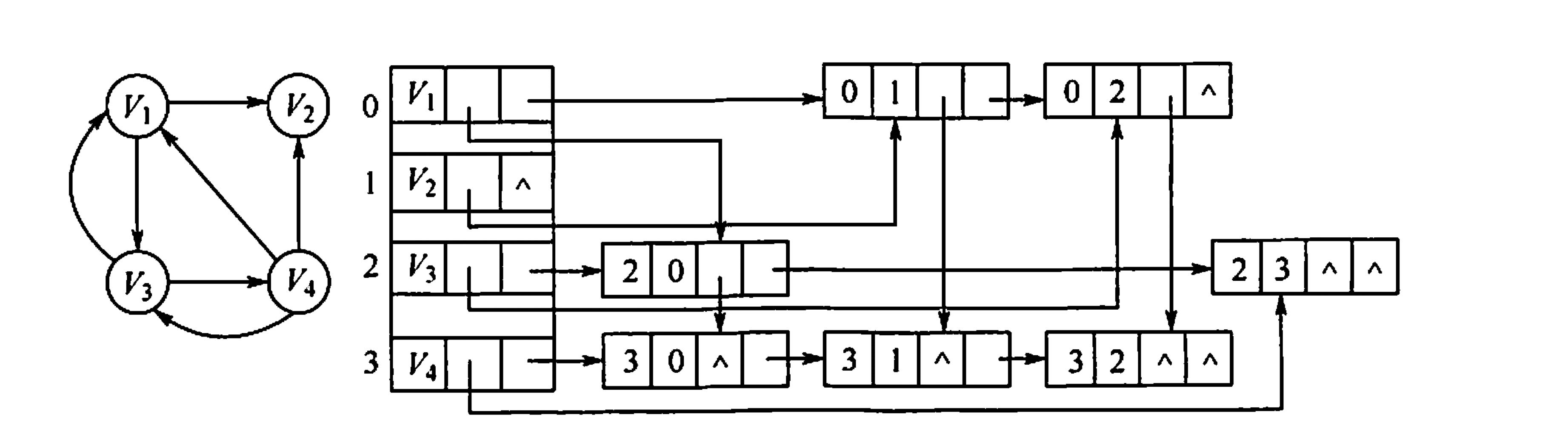
（3）十字链表法（有向图）

图的十字链表表示不唯一，但一个十字链表表示确定一个图

弧结点

tailvex headvex hlink tlink info

顶点结点

data firstin firstout

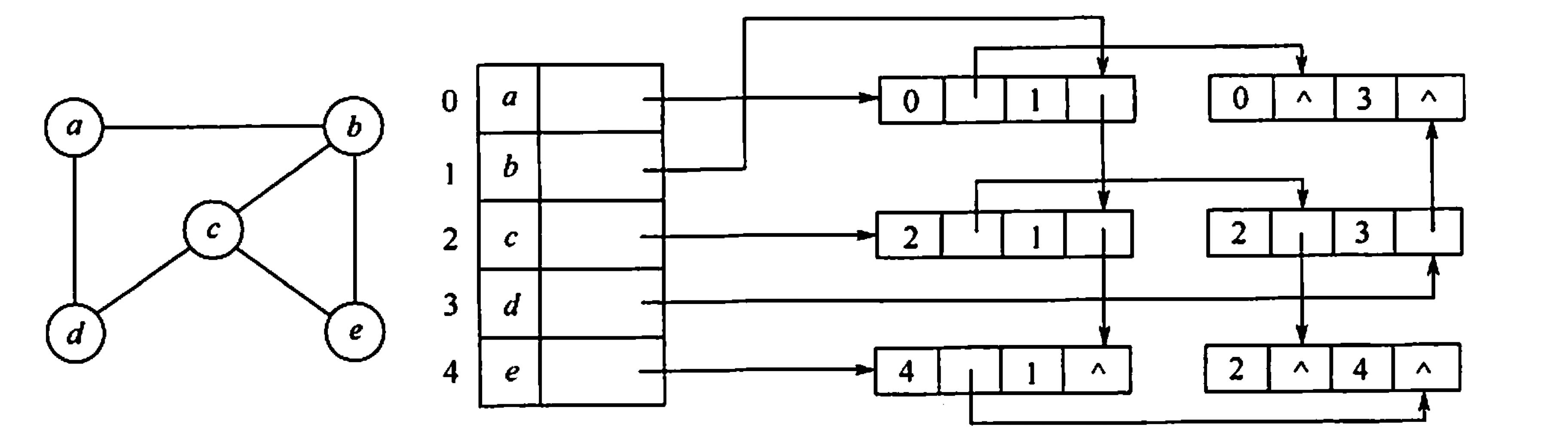
（4）邻接多重表（无向图）

顶点结点

mark ivex ilink jvex jlink info

弧顶点

data firstedge

3.基本算法实现

1
2
3
4
5
6
7
8
9
10
Adjacent(G,x,y)：判断图G是否存在边<x,y>或(x,y)。
Neighbors(G,x)：列出图G中与结点x邻接的边。
InsertVertex(G,x)：在图G中插入顶点x。
DeleteVertex(G,x)：在图G中删除顶点x。
AddEdge(G,x,y)：若无边边(x,y)或有向边<x,y>不存在，则向图G中添加该边。
RemoveEdge(G,x,y)：若无边边(x,y)或有向边<x,y>存在，则向图G中删除该边。 
FirstNeighbor(G,x)：求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回-1。
NextNeighbor(G,x,y)：假设图G中顶点y是顶点x的一个邻接点，返回除y外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1。
Get_edge_value(G,x,y)：获取图中G中边(x,y)或<x,y>对应的权值。
Set_edge_value(G,x,y,v)：设置图中G中边(x,y)或<x,y>对应的权值为v。

第二节图的遍历算法

1.广度优先搜索（BFS）

  • 邻接表：空间复杂度O(|V|) 时间复杂度O(|V|+|E|)
  • 邻接矩阵：空间复杂度O(|V|) 时间复杂度O(|V|^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
bool visited[MAX_VERTEX_NUM];				//访问标记数组
void BFSTraverse(Graph G){					//对图G进行广度优先遍历
    for(i = 0;i<G.vexnum;++i)
        visited[i] = FALSE;					//访问标记数组初始化
    InitQueue(Q);							//初始化辅助队列Q
    for(i = 0;i<G.vexnum;++i)				//从0号顶点开始遍历
        if(!visited[i])						//对每个连通分量调用一次BFS
            BFS(G,i);						//vi未访问过，从vi开始BFS
}
void BFS(Graph G,int v){					//从顶点v出发，广度优先遍历图G
    visit(v);								//访问初始顶点v
    visited[v] = TRUE;						//对v做已访问标记
    EnQueue(Q,v);							//顶点v入队列Q
    while(!osEmpty(Q)){
        DeQueue(Q,v);						//顶点v出队列
        for(w = FirstNeighbor(G,v);w>=0;w = NextNeighbor(G,v,w))	//检测v所有邻接点
            if(!visited[w]){				//w为v的尚未访问的邻接顶点
                visit(w);					//访问顶点w
                wisited[w] = TRUE;			//对w做已访问标记
                EnQueue(Q,w);				//顶点w入队列
            }//if
    }//while
}

2.深度优先搜索

  • 邻接表：空间复杂度O(|V|) 时间复杂度O(|V|+|E|)
  • 邻接矩阵：空间复杂度O(|V|) 时间复杂度O(|V|^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool visited[MAX_VERTEX_NUM];				//访问标记数组
void DFSTraverse(Graph G){					//对图G进行深度优先遍历
    for(v = 0;v<G.vexnum;++v)
        visited[v] = FALSE;					//访问标记数组初始化
    for(v = 0;v<G.vexnum;++v)				//从0号顶点开始遍历
        if(!visited[v])
            DFS(G,v);
}
void DFS(Graph G,int v){					//从顶点v出发，深度优先遍历图G
    visit(v);								//访问初始顶点v
    visited[v] = TRUE;						//对v做已访问标记
    for(w = FirstNeighbor(G,v);w>=0;w = NextNeighbor(G,v,w))
        if(!visited[w]){					//w为v的尚未访问的邻接顶点
            DFS(G,w);
        }//if
}

第三节最小生成树

1.性质

  • 最小生成树不是唯一的，即最小生成树的树形不唯一。当图G中的个边权值互不相等时，G的最小生成树时唯一的；若无向连通图G的边数比顶点数少1，即G本身就是一棵树，最小生成树就是它本身。
  • 最小生成树的边的权值之和总是唯一的
  • 最小生成树的边数为顶点数-1

2.普利姆算法（稠密图）

$$
时间复杂度：O(|V|^2)
$$

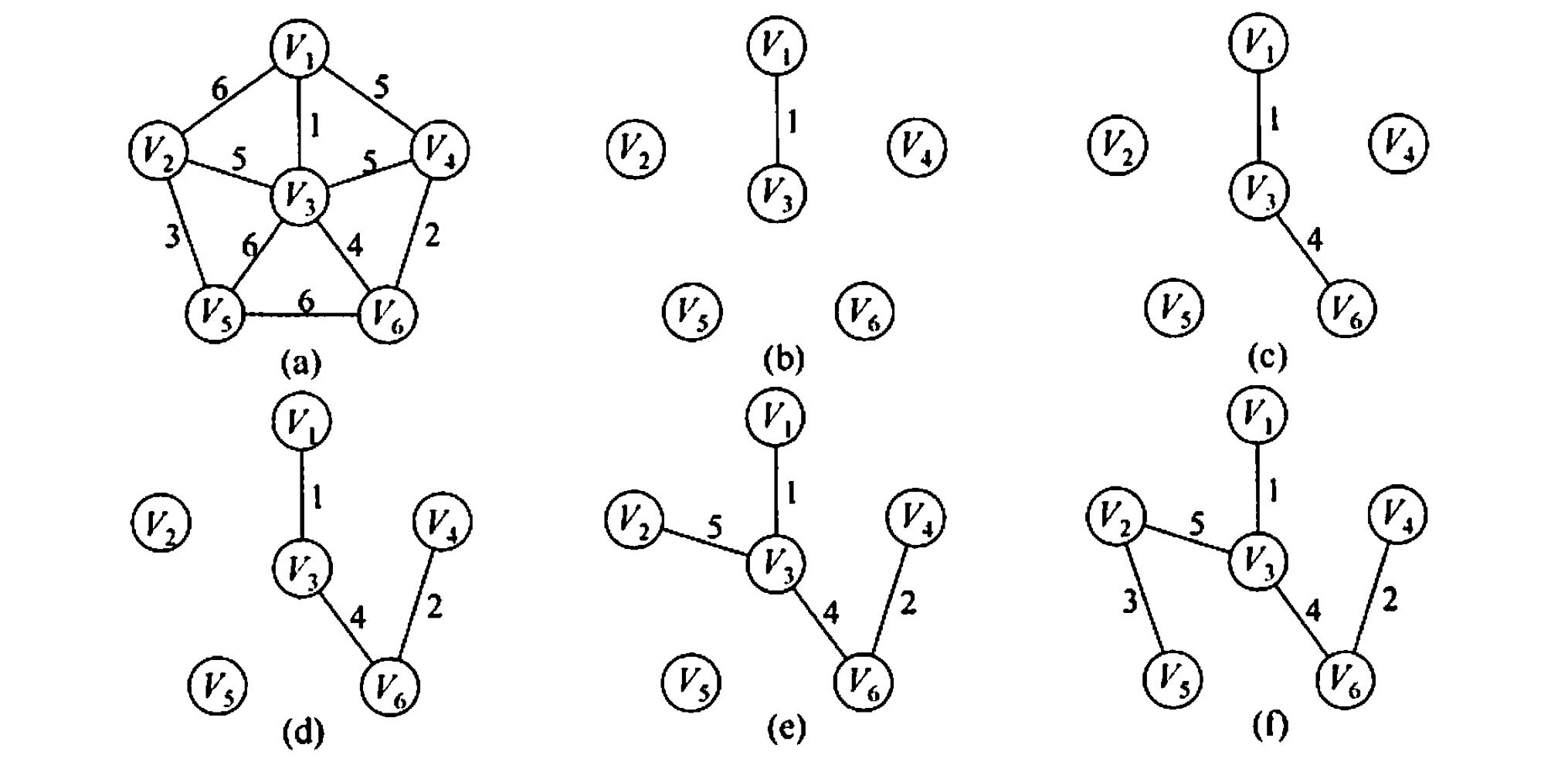
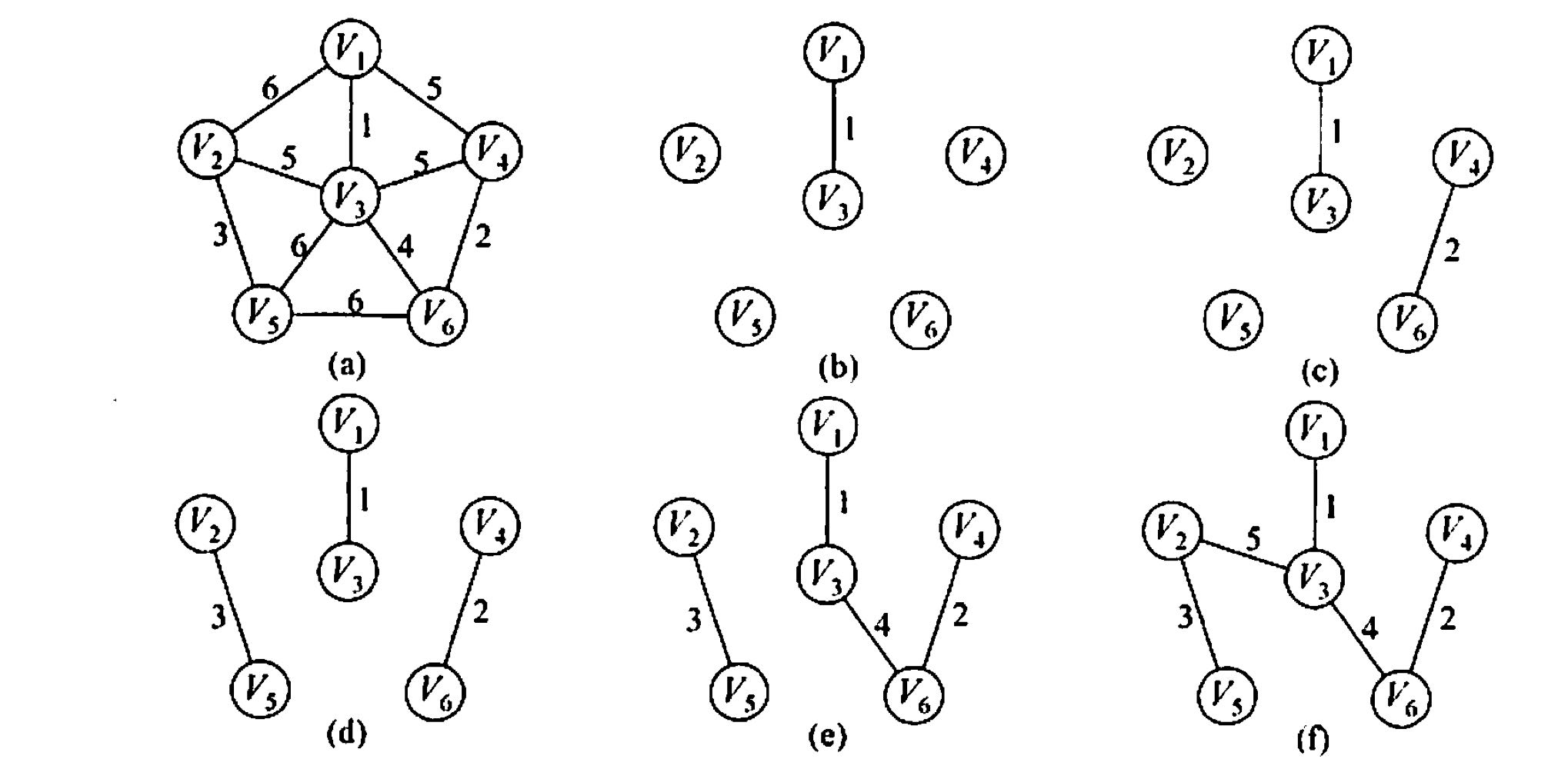
3.克鲁斯卡尔算法（稀疏图）

$$
时间复杂度：O(|E|log|E|)
$$

第四节最短路径、拓扑排序和关键路径

1.最短路径

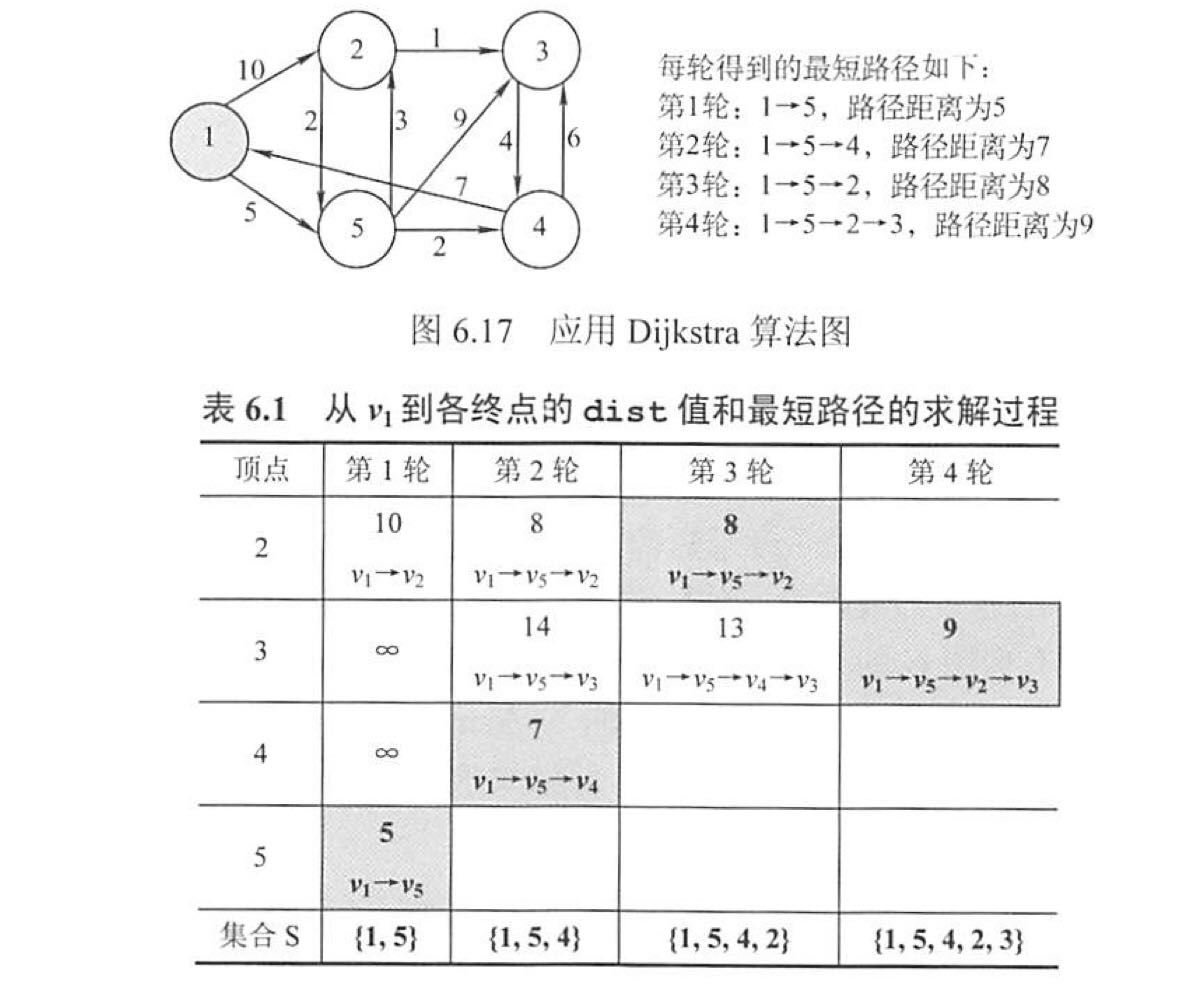
（1）Dijkstra算法(只适合正数)

$$
时间复杂度：O(|V|^2)
$$

dist[]：记录从源点v0到其他个顶点当前的最短路径长度。

path[]：path[i]表示从源点到顶点i之间的最短路径的前驱结点。

（2）Floyd算法

$$
时间复杂度：O(|V|^3)~~~~~~~~
空间复杂度：O(|V|^2)
$$

1
2
3
4
5
6
7
8
9
void Floyd(n){
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);
			}
		}
	}
}

（3）有向无环图DAG图

用来描述公共子式的表达式的有效工具

2.拓扑排序(AOV网)

graph LR;
A((1))
B((2))
C((3))
D((4))
E((5))
A-->B
A-->D
B-->C
B-->D
D-->C
C-->E
D-->E
结点号 1 2 3 4 5
初始入度 0 1 2 2 2
第一轮 0 2 1 2
第二轮 1 0 2
第三轮 0 1
第四轮 0
第五轮

$$
\begin{flalign}
&邻接表时间复杂度：O(|V|+|E|)\
&邻接矩阵时间复杂度：O(|V|^2)
\end{flalign}
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool TopologicalSort(Graph G){
    InitStack(S);							//初始化栈，存储入度为0的顶点
    for(int i = 0;i<G.vexnum;i++)
        if(indegree[i] == 0)
            Push(S,i);						//将所有入度为0的顶点进栈
    int count = 0;							//计数，记录当前已经输出的顶点数
    while(!IsEmpty(S)){						//栈不空，则存在入度为0的顶点
        Pop(S,i);							//栈顶元素出栈
        print[count++] = i;					//输出顶点i
        for(p = G.vertices[i].firstarc;p;p = p->nextarc){		
            //将所有i指向的顶点的入度-1，并且将入度减为0的顶点压入栈S
            v = p->adjvex;
            if(!(--indegree[v]))
                Push(S,v);					//入度为0，则入栈
        }
    }//while
    if(count<G.vexnum)
        return false;						//排序失败，有向图中有回路
    else
        return true;						//拓扑排序成功
}

3.关键路径(AOE网)

\begin{flalign}
&（1）事件v_k的最早发生时间ve(k)\
&指从源点v_1到顶点v_k的最长路径的长度。事件v_k的最早发生时间决定了所有从v_k开始的活动能够开工的最早时间。\
&（2）事件v_k的最迟发生时间vl(k)\
&指在不推迟整个工程完成的前提下，即保证它的后继时间v_j在其最迟发生时间vl(j)能够发生时，该事件最迟必须发生的时间。\
&（3）活动a_i的最早发生时间e(i)\
&指该活动弧的起点所表示的时间的最早发生时间\
&（4）活动a_i的最迟发生时间l(i)\
&指该活动弧的终点所表示时间的最迟发生时间与该活动所需时间之差。\
\end{flalign}