数据结构之排序

第九章排序

1.排序的概念

\begin{flalign}
&排序：按照一定的关键字，将一个序列排列成想要得到的一个新的序列。\
&稳定性：若待排序表中有两个元素 R_i 和 R_j，其对应的关键字相同即 key_i = key_j，且在排序前 R_i 在 R_j 的前面，\
&~若使用某一排序算法排序后，R_i 仍然在 R_j 的前⾯，则称这个排序算法是稳定的，否则称排序算法是不稳定的。\
&内部排序和外部排序：整个排序过程完全在内存中进行，叫做内部排序。数据量较大需要借助外部存储设备才能完成，叫做外部排序。
\end{flalign}

2.插入排序

（1）直接插入排序

① 思想：最基本的插入排序，将第i个插入到前i-1个中的适当位置。

② 时间复杂度：T(n) = O(n²*)*。

③ 空间复杂度：S(n) = O(1)。

④ 稳定性：稳定排序。

//直接插入排序
void InsertSort(int A[], int n) {	//将各元素插入已排好序的序列中,位置0的是有序的，所以从1开始
    for (int i = 1, j; i < n; ++i) {    
        if (A[i] < A[i-1]) {          //若A[i]小于前驱元素
            int temp = A[i];
            for (j = i - 1; j >= 0 && A[j] > temp; --j) {   //检查所有前面已排好序的元素
                A[j+1] = A[j];    //所有大于A[i]的元素都向后挪位
            }
            A[j+1] = temp;        //复制到插入位置
        }
    }
}

（2）折半插入排序

① 思想：因为是已经确定了前部分是有序序列，所以在查找插入位置的时候可以用折半查找的方法进行查找，提高效率。

② 时间复杂度：比较时的时间减为O(nlogn)，但是移动元素的时间耗费未变，所以总是得时间复杂度还是O(n²)。

③ 空间复杂度：S(n) = O(1)。

④ 稳定性：稳定排序。

//折半插入排序
void InsertSort2(int A[], int n) {		//依次将A[1]~A[i-1]插入到前面已排序序列
    for (int i = 1; i < n; ++i) {
        int temp = A[i];
        int low = 0, high = i - 1;
        while (low <= high) {   //折半查找
            int mid = (low + high) / 2;
            if (A[mid] > temp) 
                high = mid - 1;
            low = mid + 1;
        }
        for (int j = i-1; j >= low; --j) {		//将[low, i-1]内的元素全部右移，空出插入位置
            A[j+1] = A[j];
        }
        A[low] = temp;  //插入操作
    }
}

（3）希尔排序

① 思想：又称缩小增量排序法。把待排序序列分成若干较小的子序列，然后逐个使用直接插入排序法排序，最后再对一个较为有序的序列进行一次排序，主要是为了减少移动的次数，提高效率。原理应该就是从无序到渐渐有序，要比直接从无序到有序移动的次数会少一些。

② 时间复杂度：时间复杂度与增量序列的选择有关，最坏时间复杂度为O(n²)，当n在某个范围内时，可达O(n^1.3)。

③ 空间复杂度：S(n) = O(1)。

④ 稳定性：不稳定排序。仅适用于顺序表，不适用于链表。

//希尔排序
void ShellSort(int A[], int n) {
    for (int d = n/2; d >= 1; d /= 2) {   //步长变化
        for (int i = d, j; i < n; i += d) {
            if (A[i] < A[i-d]) {  //需将A[i]插入有序增量子表
                int temp = A[i];    //暂存元素
                for (j = i-d; j >= 0 && A[j] > temp; j -= d) {
                    A[j+d] = A[j];    //元素后移，查找插入位置
                }
                A[j+d] = temp;        //插入
            }
        }
    }
}

3.选择排序

（1）直接选择排序

① 思想：首先在所有记录中选出关键字值最小的记录，把它与第一个记录进行位置交换，然后在其余的记录中再选出关键字值次小的记录与第二个记录进行位置交换，依此类推，直到所有记录排好序。

② 时间复杂度：最好最坏平均时间复杂度为O(n²)。

③ 空间复杂度：S(n) = O(1)。

④ 稳定性：不稳定排序。

void SelectionSort(int A[],int n){
    int temp,flag;
    for(int i = 0;i < n-1;i++){
        flag = i;						//flag记录此刻需要确定最小值的位置
        for(int j = i+1;j < n;j++){			//在i+1的位置开始在后寻找最小关键字
            if(A[flag] > A[j])
                flag = j;
        }
        temp = A[flag];	A[flag] = A[i];	A[i] = temp;		//将flag的数和后面的最小关键字交换
    }
}

（2）堆排序

① 思想
作为选择排序的改进版，堆排序可以把每一趟元素的比较结果保存下来，以便我们在选择最小/大元素时对已经比较过的元素做出相应的调整。
堆排序是一种树形选择排序，在排序过程中可以把元素看成是一颗完全二叉树，每个节点都大（小）于它的两个子节点，每个节点都大于等于它的两个子节点时，就称为大顶堆，也叫堆有序； 当每个节点都小于等于它的两个子节点时，就称为小顶堆。

② 时间复杂度：最好最坏平均时间复杂度为O(nlogn)。

​ 调整时间和树的高度有关，为O(h)，在建立含n个元素的堆时，关键字的比较总次数不超过4*n，时间复杂度为O(n)

③ 空间复杂度：S(n) = O(1)。

④ 稳定性：不稳定排序。

//建立大根堆
void BuildMaxHeap(ElemType A[],int len){
    for(int i = len/2;i>0;i++)				//从i = [n/2]~1，反复调整堆
		HeapAdjust(A,i,len);
}
void HeapAdjust(ElemType A[],int k,int len){	//函数HeapAdjust将元素k为根的子树进行调整
    A[0] = A[k];						//A[0]暂存子树的根结点
    for(i = 2*k;i <= len;i++){			//沿key较大的子结点向下筛选
        if(i<len&&A[i]<A[i+1])		
            i++;						//取key较大的子结点的下标
        if(A[0] >= A[i])	break;			//筛选结束
        else{
            A[k] = A[i];				//将A[i]调整到双亲结点上
            k = i;						//修改k值，以便继续向下筛选
        }
    }
    A[k] = A[0];						//被筛选结点的值放入最终位置
}
//堆排序算法
void HeapSort(ElemType A[],int len){
    BuildMaxHeap(A,len);				//初始建堆
    for(int i = len;i>1;i++){			//n-1趟的交换和建堆过程
        Swap(A[i],A[1]);				//输出堆顶元素（和堆底元素交换）
        HeapAdjust(A,1,i-1);			//调整，把剩余的i-1个元素整理成堆
    }
}

4.交换排序

（1）冒泡排序

① 思想：两两比较相邻记录的关键字，如果反序则交换，直到没有反序的记录为止。以升序冒泡为例：每趟排序过程中通过两两比较相邻元素，将小的数字放到前面，大的数字放到后面。

② 时间复杂度：最好O(n)，最坏平均时间复杂度为O(n²)。

③ 空间复杂度：S(n) = O(1)。

④ 稳定性：稳定排序。

void BubbleSort(ElemType A[],int n){
    for(int i = 0;i < n-1;i++){
        flag = false;				//表示本趟冒泡是否发生交换的标志
        for(j = n-1;j > i;j--)		//一趟冒泡过程
            if(A[j-1]>A[j]){		//若为逆序
                swap(A[j-1],A[j]);	//交换
                flag = true;
            }
        if(flag == false)
            return;					//本趟遍历后没有发生变换，说明表已经有序
    }
}

（2）快速排序

当每次枢纽都把表等分为长度相近的两个子表时，速度是最快的

① 思想：快速排序时所有内部排序算法中平均性能最优的排序算法
在待排序的元素任取一个元素作为基准(通常选第一个元素，但最好的选择方法是从待排序元素中随机选取一个作为基准)，称为基准元素；
将待排序的元素进行分区，比基准元素大的元素放在它的右边，比其小的放在它的左边；
对左右两个分区重复以上步骤直到所有元素都是有序的。

② 时间复杂度：最好O(nlogn)，最坏时间复杂度为O(n²)。

③ 空间复杂度：最好平均情况O(logn)，最坏情况O(n)。

④ 稳定性：不稳定排序。

void QuickSort(ElemType A[],int low,int high){
    if(low<high){								//递归跳出条件
        int pos = Partitio(A,low,high);			//划分，将A[low...high]划分为满足上述条件要求的两个字表
        QuickSort(A,low,pos-1);					//依次对两个子表进行递归排序
        QuickSort(A,pos+1,high);
    }
}
void Partition(ElemType A[],int low,int high){		//一趟划分
    ElemType pivot = A[low];						//设当前表中第一个元素为枢纽，对表进行划分
    while(low<high){								//循环跳出条件
        while(low<high&&A[high]>=pivot)	--high;
        A[low] = A[high];							//将比枢纽小的元素移动到左端
        while(low<high&&A[low]<=pivot)	++low;
        A[high] = A[low];							//将比枢纽大的元素移动到右端
    }
    A[low] = pivot;								//枢纽存放到最终位置
    return low;									//返回存放枢纽的最终位置
}

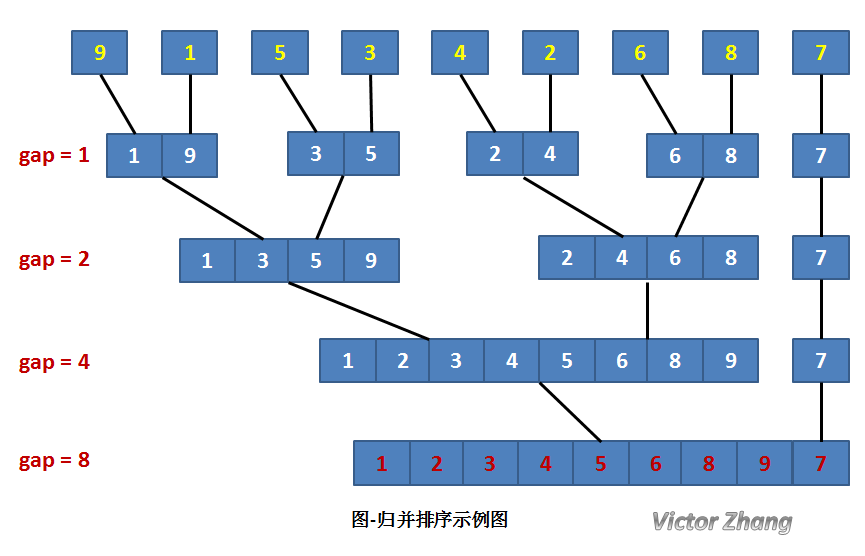
5.归并排序

① 思想：将待排序序列R[0…n-1]看成是n个长度为1的有序序列，将相邻的有序表成对归并，得到n/2个长度为2的有序表；将这些有序序列再次归并，得到n/4个长度为4的有序序列；如此反复进行下去，最后得到一个长度为n的有序序列。

② 时间复杂度：归并排序的形式就是一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的可以得出它的时间复杂度是O(nlogn)。

③ 空间复杂度：S(n) = O(n)。

④ 稳定性：稳定排序。

6.基数排序

基数排序的效率和初始序列是否有序没有关联。

① 思想：不需要比较关键字的大小。根据关键字中各位的值，通过对排序的N个元素进行若干趟“分配”与“收集”来实现排序的。

② 时间复杂度：假设在基数排序中，r为基数，d为位数。则基数排序的时间复杂度为O(d(n+r))。

③ 空间复杂度：对于任何位数上的基数进行“装桶”操作时，都需要n+r个临时空间。

④ 稳定性：稳定排序。

7.排序算法总结

排序类别	排序算法	平均情况	最好情况	最坏情况	空间复杂度	稳定性
插入排序	直接插入排序	O(n²)	O(n)	O(n²)	O(1)	稳定
	折半插入排序	O(n²)	O(n)	O(n²)	O(1)	稳定
	希尔排序		O(n²)		O(1)	不稳定
选择排序	直接选择排序	O(n²)	O(n²)	O(n²)	O(1)	不稳定
	堆排序	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	不稳定
交换排序	冒泡排序	O(n²)	O(n)	O(n²)	O(1)	稳定
	快速排序	O(nlogn)	O(nlogn)	O(n²)	O(logn)	不稳定
归并排序	归并排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	稳定
基数排序	基数排序	O(d(n+r))	O(d(n+r))	O(d(n+r))	O(n+r)	稳定